PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
GC
2
GW
21 tháng 9 2021
Đáp án :
\(-3\notinℕ\)
\(-3\in Z\)
\(-3\in Q\)
\(\frac{-2}{3}\notin Z\)
\(\frac{-2}{3}\in Q\)
\(N\subset Z\subset Q\)
21 tháng 9 2021
tả lời minh ko biết đánh kí hiệu nên là vậy nha
-3 ko thuộc N / -3 thuộc Z / -3 thuộc Q
-2/3 ko thuộc Q / -2/3 thuộc Q / N là tập hợp con của Z mà Z lại là tập hợp con của Q
chúc bn có 1 năm học mới vui vẻ
1 tháng 5 2019
Cho hai tập hợp A = {a, b}; B = {b, x, y}. Điền kí hiệu thích hợp vào ô vuông:
x ..\(\notin\)... A ; y ...\(\in\).. B ; b ...\(\in\).. A ; b ..\(\in\)...B
1 tháng 5 2019
x ...\(\notin\).. A ; y ...\(\in\).. B ; b \(\notin\)..... A ; b ...\(\in\)..B
TM
1
TM
6
18 tháng 3 2018
Thu gọn rồi tính giá trị của đa thức P tại x = 0,5 và y = 1:
20 tháng 9 2017
a) 2n = 16/2=8= 23 => n =3
b) (-3)n = (-27).81 =(-3)3.34= (-3)7 => n = 7
c) 4 =22= 23n.2n = 23n-n = 22n => n =1
TM
5
21 tháng 11 2017
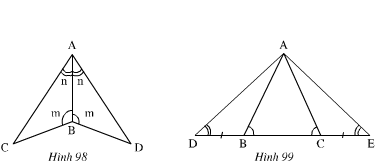
nh 98): Xét ΔABC và ΔABD có:
Nên ΔABC = ΔABD (g.c.g)
- Hình 99): Ta có:
Xét ΔABD và ΔACE có:
Nên ΔABD = ΔACE ( g.c.g)
Xét ΔADC và ΔAEB có:
DC = EB (Vì DC = DB + BC ; EB = EC + BC mà DB = EC)
Nên ΔADC = ΔAEB (g.c.g)
TH
21 tháng 11 2017
Xem hình 98)
∆ABC và ∆ABD có:
ˆA1A1^=ˆA2A2^(gt)
AB là cạnh chung.
ˆB1B1^=ˆB2B2^(gt)
Nên ∆ABC=∆ABD(g.c.g)
Xem hình 99)
Ta có:
ˆB1B1^+ˆB2B2^=1800 (Hai góc kề bù).
ˆC1C1^+ ˆC2C2^=1800 (Hai góc kề bù)
Mà ˆB2B2^=ˆC2C2^(gt)
Nên ˆB1B1^=ˆC1C1^
* ∆ABD và ∆ACE có:
ˆB1B1^=ˆC1C1^(cmt)
BD=EC(gt)
ˆDD^ = ˆEE^(gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
ˆDD^=ˆEE^(gt)
ˆC2C2^=ˆB2B2^(gt)
DC=EB
Nên ∆ADC=∆AEB(g.c.g)
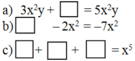
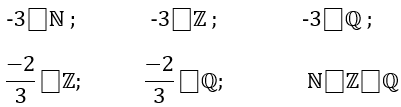
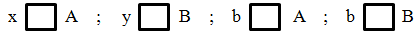
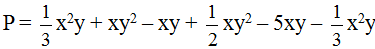
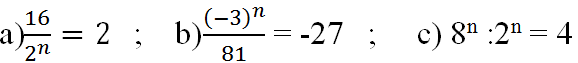
Có nhiều cách điền vào 3 ô trống ở câu c chẳng hạn :
10x5+ (-4x5) +(-5x5) = x5
Hoặc x5+3x5+ (-3x5) = x5
Hoặc x5+3+(-3) = x5
…