Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,Gọi phân giác ứng với cạnh huyền là AD
=>BD/CD=3/4
vì AD là p,giac góc A=>BD/CD=AB/AC=3/4
=>AB=3/4AC
Aps dụng định lí Py-ta-go:=>AB^2+AC^2=BC^2=100
<=>(3/4AC)^2+AC^2=100
<=>25/16AC^2=100
<=>AC=8(cm)
=>AB=3/4AC=6(cm)
b, Xét tam giác ABC có góc A = 90độ và AH là đường cao (gt) => Áp dụng hệ thức lượng tam giác vuông ta có:
1/(AH²) = 1/(AB²) + 1/(AC²)
<=> 1/(AH²) = 1/(6²) + 1/(8²)
<=> 1/(AH²) = 1/36 + 1/64
<=> 1/(AH²) = 25/576
=> 1/AH = 5/24
=> AH = 24/5 =4,8(cm)

a: \(AH=2\sqrt{6}\left(cm\right)\)
\(AB=2\sqrt{10}\left(cm\right)\)
\(AC=2\sqrt{15}\left(cm\right)\)

a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AC^2=CH\cdot BC\\AB^2=BH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=2\sqrt{6}\left(cm\right)\\AC=2\sqrt{15}\left(cm\right)\\AB=2\sqrt{10}\left(cm\right)\end{matrix}\right.\)

AB/AC=5/12
=>AB/5=AC/12=k
=>AB=5k; AC=12k
ΔABC vuông tại A
=>AB^2+AC^2=BC^2
=>25k^2+144k^2=26^2
=>169k^2=26^2
=>k^2=4
=>k=2
=>AB=10cm; AC=24cm
ΔABC vuông tại A có AH là đường cao
nên BH*BC=BA^2; CH*CB=CA^2
=>BH=10^2/26=100/26=50/13(cm); CH=24^2/26=288/13(cm)
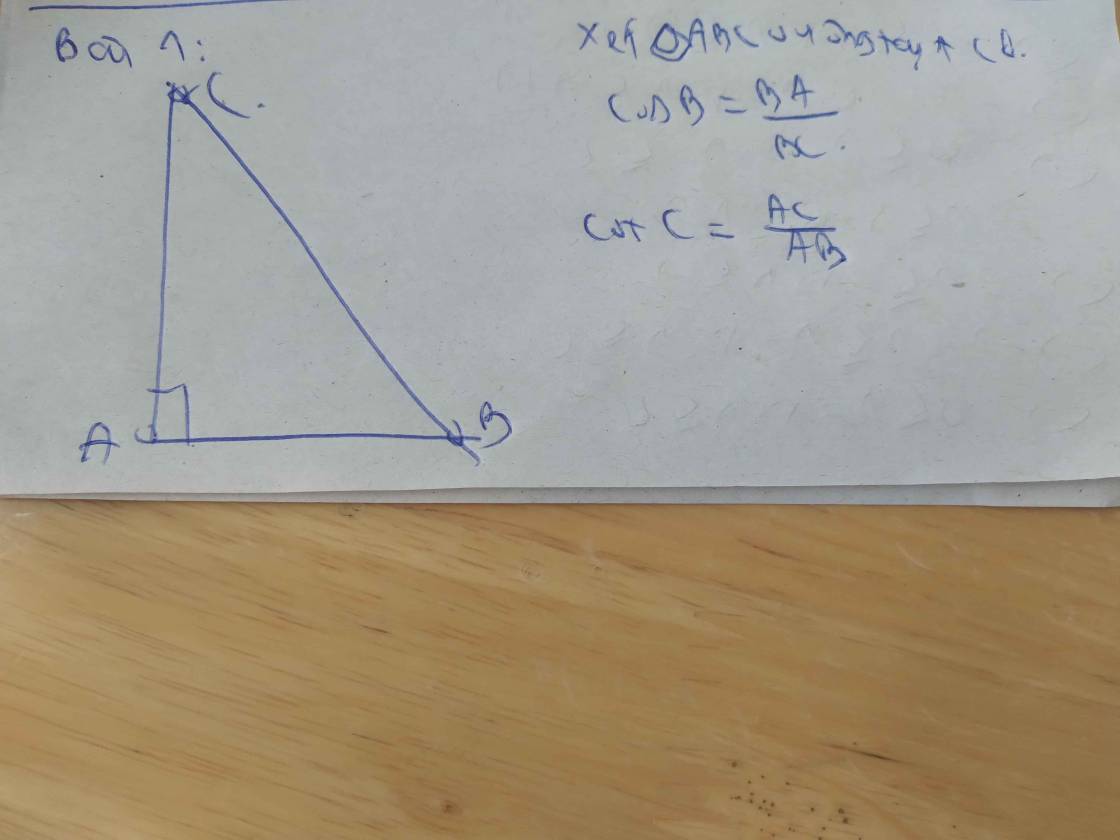

Giả sử AC là cạnh lớn hơn
Theo định lý Pitago: \(AB^2+AC^2=BC^2\Leftrightarrow AB^2+AC^2=100\) (1)
Gọi D là chân đường phân giác trong góc A trên BC
Theo giả thiết: \(\dfrac{BD}{CD}=\dfrac{3}{4}\)
Mà theo định lý phân giác: \(\dfrac{BD}{CD}=\dfrac{AB}{AC}\Rightarrow\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow AB=\dfrac{3}{4}AC\) (2)
Thế (2) vào (1):
\(\left(\dfrac{3}{4}AC\right)^2+AC^2=100\Rightarrow AC^2=64\)
\(\Rightarrow AC=8\left(cm\right)\)
\(AB=\dfrac{3}{4}AC=\dfrac{3}{4}.8=6\left(cm\right)\)