Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\text{a) }\dfrac{3}{x^2+5x+4}+\dfrac{2}{x^2+10x+24}=\dfrac{4}{3}+\dfrac{9}{x^2+3x-18}\\ ĐKXĐ:x\ne-1;x\ne-3;x\ne-4;x\ne-6\\ \Rightarrow\dfrac{3}{x^2+4x+x+4}+\dfrac{2}{x^2+6x+4x+24}=\dfrac{4}{3}+\dfrac{9}{x^2+6x-3x-18}\\ \Rightarrow\dfrac{3}{x\left(x+4\right)+\left(x+4\right)}+\dfrac{2}{x\left(x+6\right)+4\left(x+6\right)}=\dfrac{4}{3}+\dfrac{9}{x\left(x+6\right)-3\left(x+6\right)}\\ \Rightarrow\dfrac{3}{\left(x+1\right)\left(x+4\right)}+\dfrac{2}{\left(x+4\right)\left(x+6\right)}=\dfrac{4}{3}+\dfrac{9}{\left(x-3\right)\left(x+6\right)}\)\(\Rightarrow\dfrac{1}{x+1}-\dfrac{1}{x+4}+\dfrac{1}{x+4}-\dfrac{1}{x+6}=\dfrac{4}{3}+\dfrac{1}{x-3}-\dfrac{1}{x+6}\\ \Rightarrow\dfrac{1}{x+1}-\dfrac{1}{x+6}-\dfrac{1}{x-3}+\dfrac{1}{x+6}=\dfrac{4}{3}\\ \Rightarrow\dfrac{1}{x+1}-\dfrac{1}{x-3}=\dfrac{4}{3}\\ \Rightarrow\dfrac{3\left(x-3\right)}{3\left(x+1\right)\left(x-3\right)}-\dfrac{3\left(x+1\right)}{3\left(x+1\right)\left(x-3\right)}=\dfrac{4\left(x+1\right)\left(x-3\right)}{3\left(x+1\right)\left(x-3\right)}\\ \Rightarrow3x-9-3x-3=4\left(x^2-2x-3\right)\\ \Leftrightarrow4x^2-8x-12=-12\\ \Leftrightarrow4x^2-8x=0\\ \Leftrightarrow4x\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}4x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)Vậy phương trình có tập nghiệm \(S=\left\{0;2\right\}\)

2) Ta có: \(\dfrac{x+4}{5}-x+4=\dfrac{x}{3}-\dfrac{x-2}{2}\)
\(\Leftrightarrow\dfrac{6\left(x+4\right)}{30}-\dfrac{30\left(x-4\right)}{30}=\dfrac{10x}{30}-\dfrac{15\left(x-2\right)}{30}\)
\(\Leftrightarrow6x+24-30x+120=10x-15x+30\)
\(\Leftrightarrow-24x+144=-5x+30\)
\(\Leftrightarrow-24x+144+5x-30=0\)
\(\Leftrightarrow-19x+114=0\)
\(\Leftrightarrow-19x=-114\)
hay x=6
Vậy: x=6
3) Ta có: \(\dfrac{10x+3}{12}=1+\dfrac{6+8x}{9}\)
\(\Leftrightarrow\dfrac{3\left(10x+3\right)}{36}=\dfrac{36}{36}+\dfrac{4\left(6+8x\right)}{36}\)
\(\Leftrightarrow30x+9=36+24+32x\)
\(\Leftrightarrow30x+9-60-32x=0\)
\(\Leftrightarrow-2x-51=0\)
\(\Leftrightarrow-2x=51\)
hay \(x=-\dfrac{51}{2}\)
Vậy: \(x=-\dfrac{51}{2}\)
4) Ta có: \(\dfrac{x+1}{3}-\dfrac{x-2}{6}=\dfrac{2x-1}{2}\)
\(\Leftrightarrow\dfrac{2\left(x+1\right)}{6}-\dfrac{x-2}{6}=\dfrac{3\left(2x-1\right)}{6}\)
\(\Leftrightarrow2x+2-x+2=6x-3\)
\(\Leftrightarrow x+4-6x+3=0\)
\(\Leftrightarrow-5x+7=0\)
\(\Leftrightarrow-5x=-7\)
hay \(x=\dfrac{7}{5}\)
Vậy: \(x=\dfrac{7}{5}\)
1) \(\dfrac{5x-2}{3}=\dfrac{5-3x}{2}\)
\(2\left(5x-2\right)=3\left(5-3x\right)\)
\(10x-4=15-9x\)
\(10x+9x=15+4\)
\(19x=19\)
\(x=1\)
Vậy \(x=1\)

f: =>\(\dfrac{14}{3\left(x-4\right)}-\dfrac{x+2}{x-4}=\dfrac{-3}{2\left(x-4\right)}-\dfrac{5}{6}\)
=>28-6(x+2)=-9-5(x-4)
=>28-6x-12=-9-5x+20
=>-6x+16=-5x+11
=>-x=-5
=>x=5
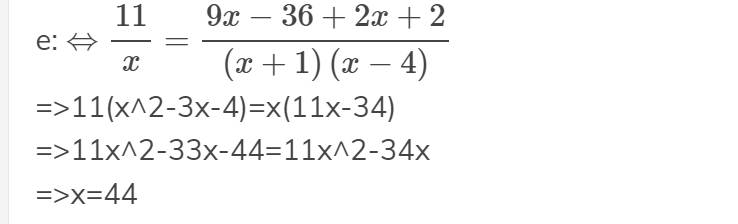

d: =>\(\dfrac{12x+1}{11x-4}=\dfrac{20x+17-20x+8}{18}=\dfrac{25}{18}\)
=>25(11x-4)=18(12x+1)
=>275x-100=216x+18
=>59x=118
=>x=2
f: =>\(\dfrac{14}{3\left(x-4\right)}-\dfrac{x+2}{x-4}=\dfrac{-3}{2\left(x-4\right)}-\dfrac{5}{6}\)
=>28-6(x+2)=-9-5(x-4)
=>28-6x-12=-9-5x+20
=>-6x+16=-5x+11
=>-x=-5
=>x=5
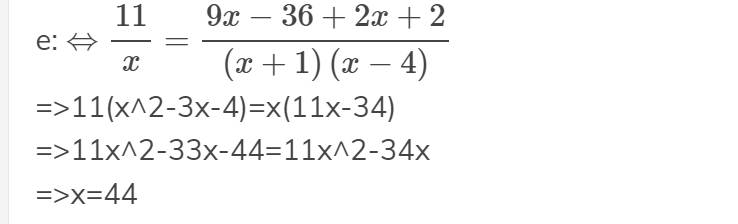

1: Ta có: \(\dfrac{x-4}{3}+2x=\dfrac{4x-2}{6}\)
\(\Leftrightarrow2x-8+12x=4x-2\)
\(\Leftrightarrow10x=6\)
hay \(x=\dfrac{3}{5}\)
2: Ta có: \(\dfrac{5x-2}{5}-2=\dfrac{1-2x}{3}\)
\(\Leftrightarrow15x-6-30=10-20x\)
\(\Leftrightarrow35x=46\)
hay \(x=\dfrac{46}{35}\)
3: Ta có: \(\dfrac{x-2}{2}-\dfrac{2}{3}=x-1\)
\(\Leftrightarrow3x-6-4=6x-6\)
\(\Leftrightarrow-3x=4\)
hay \(x=-\dfrac{4}{3}\)

1) điều kiện xác định : \(x\notin\left\{-1;-2;-3;-4\right\}\)
ta có : \(\dfrac{1}{x^2+3x+2}+\dfrac{1}{x^2+5x+6}+\dfrac{1}{x^2+7x+12}=\dfrac{1}{6}\)
\(\Leftrightarrow\dfrac{1}{\left(x+1\right)\left(x+2\right)}+\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+4\right)}=\dfrac{1}{6}\) \(\Leftrightarrow\dfrac{\left(x+3\right)\left(x+4\right)+\left(x+1\right)\left(x+4\right)+\left(x+1\right)\left(x+2\right)}{\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)}=\dfrac{1}{6}\)\(\Leftrightarrow\dfrac{x^2+7x+12+x^2+5x+4+x^2+3x+2}{\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)}=\dfrac{1}{6}\)
\(\Leftrightarrow\dfrac{3x^2+15x+18}{\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)}=\dfrac{1}{6}\)
\(\Leftrightarrow6\left(3x^2+15x+18\right)=\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)\)
\(\Leftrightarrow18\left(x^2+5x+6\right)=\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)\)
\(\Leftrightarrow18\left(x+2\right)\left(x+3\right)=\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)\)
\(\Leftrightarrow18=\left(x+1\right)\left(x+4\right)\) ( vì điều kiện xác định )
\(\Leftrightarrow18=x^2+5x+4\Leftrightarrow x^2+5x-14=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+7\right)=0\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+7=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-7\end{matrix}\right.\left(tmđk\right)\)
vậy \(x=2\) hoặc \(x=-7\) mấy câu kia lm tương tự nha bn

1: Ta có: \(\dfrac{3}{x-3}+\dfrac{4}{x+3}=\dfrac{3x-7}{x^2-9}\)
\(\Leftrightarrow\dfrac{3x+9}{\left(x-3\right)\left(x+3\right)}+\dfrac{4x-12}{\left(x-3\right)\left(x+3\right)}=\dfrac{3x-7}{\left(x-3\right)\left(x+3\right)}\)
Suy ra: \(3x+9+4x-12=3x-7\)
\(\Leftrightarrow4x=-7+12-9=-4\)
hay \(x=-1\left(nhận\right)\)
2: Ta có: \(\dfrac{3}{x-4}-\dfrac{4}{x+4}=\dfrac{3x-4}{x^2-16}\)
\(\Leftrightarrow\dfrac{3x+12}{\left(x-4\right)\left(x+4\right)}-\dfrac{4x-16}{\left(x+4\right)\left(x-4\right)}=\dfrac{3x-4}{\left(x-4\right)\left(x+4\right)}\)
Suy ra: \(3x+12-4x+16=3x-4\)
\(\Leftrightarrow28-4x=-4\)
\(\Leftrightarrow4x=32\)
hay \(x=8\left(tm\right)\)
3: Ta có: \(\dfrac{5x^2-12}{x^2-1}+\dfrac{3}{x-1}=\dfrac{5x}{x+1}\)
Suy ra: \(5x^2-12+3x+3=5x^2-5x\)
\(\Leftrightarrow3x-9+5x=0\)
\(\Leftrightarrow8x=9\)
hay \(x=\dfrac{9}{8}\left(nhận\right)\)

1: Ta có: \(\dfrac{5x+1}{8}-\dfrac{x-2}{4}=\dfrac{1}{2}\)
\(\Leftrightarrow5x+1-2\left(x-2\right)=4\)
\(\Leftrightarrow5x+1-2x+4=4\)
\(\Leftrightarrow3x=-1\)
hay \(x=-\dfrac{1}{3}\)
2: Ta có: \(\dfrac{x+3}{4}+\dfrac{1-3x}{3}=\dfrac{-x+1}{18}\)
\(\Leftrightarrow9x+27+12-36x=-2x+2\)
\(\Leftrightarrow-27x+2x=2-39\)
hay \(x=\dfrac{37}{25}\)
3: Ta có: \(\dfrac{x+2}{4}-\dfrac{5x}{6}=\dfrac{1-x}{3}\)
\(\Leftrightarrow3x+6-10x=4-4x\)
\(\Leftrightarrow-7x+4x=4-6=-2\)
hay \(x=\dfrac{2}{3}\)
4: Ta có: \(\dfrac{x-3}{2}-\dfrac{x+1}{10}=\dfrac{x-2}{5}\)
\(\Leftrightarrow5x-15-x-1=2x-4\)
\(\Leftrightarrow4x-2x=-4+16=12\)
hay x=6
5: Ta có: \(\dfrac{4x+1}{4}-\dfrac{9x-5}{12}+\dfrac{x-2}{3}=0\)
\(\Leftrightarrow12x+3-9x+5+4x-8=0\)
\(\Leftrightarrow7x=0\)
hay x=0

a)\(\dfrac{3}{x^2+5x+4}+\dfrac{2}{x^2+10x+24}=\dfrac{4}{3}+\dfrac{9}{x^2+3x-18}\left(đkxđ:x\ne-1;-4;-6;3\right)\)
\(\Leftrightarrow\dfrac{3}{\left(x+1\right)\left(x+4\right)}+\dfrac{2}{\left(x+4\right)\left(x+6\right)}=\dfrac{4}{3}+\dfrac{9}{\left(x+6\right)\left(x-3\right)}\)
\(\Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x+4}+\dfrac{1}{x+4}-\dfrac{1}{x+6}=\dfrac{4}{3}+\dfrac{1}{x-3}-\dfrac{1}{x+6}\)
\(\Leftrightarrow\dfrac{1}{x+1}=\dfrac{4}{3}+\dfrac{1}{x-3}\)
\(\Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x-3}=\dfrac{4}{3}\)
\(\Leftrightarrow\dfrac{-4}{\left(x+1\right)\left(x-3\right)}=\dfrac{4}{3}\)
\(\Leftrightarrow\left(x+1\right)\left(3-x\right)=3\)
\(\Leftrightarrow2x-x^2+3=3\)
\(\Leftrightarrow x^2-2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\left(tm\right)\)
b)\(x^2-y^2+2x-4y-10=0\)
\(\Leftrightarrow x^2+2x+1-y^2-4y-4-7=0\)
\(\Leftrightarrow\left(x+1\right)^2-\left(y+2\right)^2=7\)
\(\Leftrightarrow\left(x-y-1\right)\left(x+y+3\right)=7\)
Mà x,yEN*=>x-y-1<x+y+3
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-y-1=1\\x+y+3=7\end{matrix}\right.\\\left\{{}\begin{matrix}x-y-1=-7\\x+y+3=-1\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)
Vậy ...
\(\dfrac{3}{\left(x+1\right)\left(x+4\right)}+\dfrac{2}{\left(x+4\right)\left(x+6\right)}=\dfrac{9}{\left(x-3\right)\left(x+6\right)}=\dfrac{4}{3}\)
=> \(\dfrac{1}{x+1}-\dfrac{1}{x+4}+\dfrac{1}{x+4}-\dfrac{1}{x+6}=\dfrac{1}{x-3}-\dfrac{1}{x+6}=\dfrac{4}{3}\)
=> \(\dfrac{1}{x+1}-\dfrac{1}{x+6}-\dfrac{1}{x-3}+\dfrac{1}{x+6}=0\)
=> \(\dfrac{1}{x+1}-\dfrac{1}{x-3}=0\)
Ma \(\dfrac{1}{x+1}-\dfrac{1}{x-3}=\dfrac{4}{3}\)
=> pt vo nghiem
\(\dfrac{1}{x+1}-\dfrac{1}{x+4}+\dfrac{1}{x+4}-\dfrac{1}{x+6}-\dfrac{1}{x+3}+\dfrac{1}{x+6}=\dfrac{4}{3}\)
=> \(\dfrac{1}{x+1}-\dfrac{1}{x+3}=\dfrac{4}{3}\)
=> \(\dfrac{2}{\left(x+1\right)\left(x+3\right)}=\dfrac{4}{3}\)
=> 4(x+1)(x+3)=6
=> 4(x2+4x+3)=6
=> 4x2+16x+6=0
=> (4x2+16x+16)-10=0
=> (2x+4)2=10
=> \(\left[{}\begin{matrix}2x+4=\sqrt{10}\\2x+4=-\sqrt{10}\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}x=\dfrac{\sqrt{10}-4}{2}\\x=\dfrac{-\sqrt{10}-4}{2}\end{matrix}\right.\)