Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án: A.
H0 = 2,10-6.3,7.1010 = 7,4.104Bq;
H = 502V phân rã/phút = 8,37V Bq (V thể tích của máu tính theo cm3 )
H = H0 .2-t/T = H0.2-0,5 → 2-0,5 = H/H0 → 8,37 V = 7,4.104.2-0,5
V = 6251,6 cm3 = 6,25 dm3 = 6,25 lit.
Đáp án B.
Trong thể tích V 0 = 10 c m 3 = 10 - 2 lít dung dịch với nồng độ 10-3 mol/lít có số mol là n = 10 - 5 mol và có khối lượng là: m 0 = n A = 24 . 10 - 5 g.
Vì N 11 24 a là chất phóng xạ nên sau 6 giờ lượng N 11 24 a còn lại là:
m = m 0 e - λ t = 24 . e ln 2 T t = 18 . 10 - 5 ( g )
Trong thể tích V 0 = 10 c m 3 máu lấy ra có 1 , 875 . 10 - 8 mol của Na, tương ứng với khối lượng chất phóng xạ: m' = n'.A = 1 , 875 . 10 - 8 .24 = 45 . 10 - 8 (g)
Vậy thể tích máu là:
V = m m ' . V 0 = 18 . 10 - 5 45 . 10 - 8 . 10 = 4 . 10 3 c m 3 = 4 ( L í t )
Đáp án B.
Trong thể tích V 0 = 10 c m 3 = 10 - 2 lít dung dịch với nồng độ 10 - 3 mol/lít có số mol là n = 10 - 5 m o l và có khối lượng là: m 0 = n A = 24 . 10 - 5 g .
Vì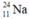 
là chất phóng xạ nên sau 6 giờ lượng 
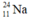còn lại là:
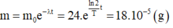
Trong thể tích
V
0
=
10
c
m
3
máu lấy ra có
1
,
875
.
10
-
8
m
o
l
của Na, tương ứng với khối lượng chất phóng xạ:
Vậy thể tích máu là:
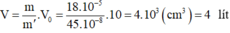
Khối lượng chất phóng xạ đã bị phân rã là
\(\Delta m = m_0(1-2^{-\frac{t}{T}}) \)
=> \(\frac{\Delta m }{m_0}= 0,75 =1- 2^{-\frac{t}{T}}\)
=> \(t = -T\ln_20,25 = 30h.\)
t = 0 lúc mới chặt hiện tại t thời gian
Xét tỉ số giữa độ phóng xạ ở thời điểm \(t\) và độ phóng xạ ban đầu ( không cần chuyển đơn vị của độ phóng xạ từ phân rã / phút sang phân rã / giây vì dùng phép chia hai độ phóng xạ cho nhau.)
\(\frac{H}{H_0}= 2^{-\frac{t}{T}}= \frac{1}{8}= 2^{-3}.\)
=> \(t = 3T= 3.5730 = 17190 \)(năm).
Khối lượng Rn còn lại sau 1,5 chu kì là: \(m=m_0.2^{-1,5}=2.2^{-1,5}(g)\)
Độ phóng xạ là: \(H=N.\lambda=\dfrac{2.2^{-1,5}}{222}.6,02.10^{23}.\dfrac{\ln 2}{3,8.24.3600}=...\)
Số hạt nhân ban đầu
\(N_0= \frac{H_0}{\lambda}\)
Khối lượng ứng cới độ phóng xạ \(H_0\) là
\(m_0 = nA= \frac{N_0}{N_A}A= \frac{H_0}{N_A}= \frac{5.3,7.10^{10}.14}{6,02.10^{23} \frac{\ln 2}{5570.365.24.3600}}= 1,09g.\)
Số hạt nhân chưa phóng xạ chính là số hạt nhân còn lại
\(N= N_0 2^{-\frac{t}{T}}= N_0 .2^{-4}= \frac{1}{16}N_0.\)
1 hạt nhân \(_6^{14}C\) bị phân rã tạo thành 1 hạt nhân \(_7^{14}N\).
Tỉ số giữa số nguyên tử đã bị phóng xạ và số nguyên tử ban đầu là
\(\frac{\Delta N}{N_0}= 1-2^{-\frac{t}{T}}= 0,875.\)
=> \(2^{-\frac{t}{T}}= 0,125= 2^{-3}.\)
=> \(t = 3T = 16710\)(năm).
Đáp án B