Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta phân tích 847 - 840 + 7 = 84.10 + 7 suy ra có 84 bậc số điện. Số tiền ông A phải trả cho bậc 1 là 10.500 đồng.
Số tiền ông A phải trả cho bậc 2 là 10.(500 + 500.2,5%) đồng.
Số tiền ông A phải trả cho bậc 3 là 10.[500.(1 + 2,5%) + 500.(1 + 2,5%).2,5%] = 10.500. 1 , 025 2 đồng.
… … …
Số tiền ông A phải trả cho bậc 84 là 10 . 500 . 1 , 025 83 đồng.
Vậy tổng số tiền ông A phải trả là T = 5000 + 5000 . 1 , 025 + . . . + 5000 . 1 , 025 83 + 7 . 500 . 1 , 025 84 .
Xét cấp số nhân có u 1 = 1 ; u n = 1 , 025 83 và q = 1 , 025 ⇒ S = 1 + 1 , 025 + 1 , 025 2 + . . . + 1 , 025 83 = u 1 . 1 - q n 1 - q
Suy ra S = 1 - 1 , 025 84 1 - 1 , 025 . Vậy T = 5000 . 1 - 1 , 025 84 1 - 1 , 025 + 7 . 500 . 1 , 025 84 ≈ 1419455 , 83 . .

Độ cao của các bậc thang thứ n của tòa nhà được tính theo công thức: u = 0 , 95 + n - 1 . 0 , 15 .
Độ cao của bậc thứ 8 so với mặt đất là: u 8 = 0 , 95 + 7 . 0 , 15 = 2
Chọn B.

Giải: Biết chữ số hàng trăm, hàng chục, hàng đơn vị là 3 số tự nhiên liên tiếp tăng dần nên các số đó là: 123, 234,345,456,567,789. Và khi viết theo thứ tự ngược lại thì các số đó là: 321,432,543,654,765,987.
Số đó sẽ tăng lên là: 321 - 123 = 198
432 - 234 = 198
Tương tự như thế
.......................
Đáp số: 198

Đổ 8 lít từ thùng một sang thùng hai thì tổng không thay đổi. Vậy:
Số dầu thùng một là :
( 60 : 3 ) + 8 = 28 ( lít )
Số đầu thùng hai là :
60 - 28 = 32 ( lít )
Đáp số : thùng 1 : 28 lít
thùng 2 :32 lít
gọi x là số lít dầu ở thunhf thứ nhất, y là số lít dầu ở thùng thứ 2 ta có:
x+y=60 => x=60-y
Theo đề bài ta có
2(x-8)=(y+8)
=>2(60-y-8)=y+8
<=> 104-2y=y+8
<=> -2y-y=8-104
<=> -3y =-96
<=> y=32
=> x= 60 -y=60-32=28
Vậy thùng 1 có 28 lít dầu
thùng 2 có 32 lít dầu

Đáp án B
Gọi A là số tiền gốc ban đầu, lãi suất r/năm, số tiền gửi thêm là a (triệu đồng)
Sau năm đầu tiên, số tiền cả gốc lẫn lãi mà ông Minh nhận đc là A(1+r)
Sau năm thứ 2, cả gốc và lãi ông nhận được là
![]()
Sau năm thứ 3, cả gốc và lãi ông nhận được:
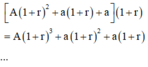
Sau năm thứ n, ông Minh nhận được số tiền:
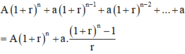
Thay số: sau 10 năm ông Minh nhận về cả gốc lẫn lãi là
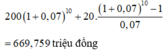
Đáp án B
Gọi A là số tiền gốc ban đầu, lãi suất r/năm, số tiền gửi thêm là a (triệu đồng)
Sau năm đầu tiên, số tiền cả gốc lẫn lãi mà ông Minh nhận đc là A(1+r)
Sau năm thứ 2, cả gốc và lãi ông nhận được là
![]()
Sau năm thứ 3, cả gốc và lãi ông nhận được:
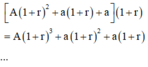
Sau năm thứ n, ông Minh nhận được số tiền:
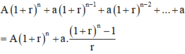
Thay số: sau 10 năm ông Minh nhận về cả gốc lẫn lãi là
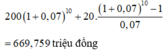

Đáp án C
Gọi A là số tiền gốc ban đầu, lãi suất r / năm, số tiền gửi thêm là a (triệu đồng).
Sau năm đầu tiên, số tiền cả gốc lẫn lãi mà ông Minh nhận được là: A 1 + r
Sau năm thứ 2, cả gốc và lãi ông nhận được là: A 1 + r + a 1 + r = A 1 + r 2 + a 1 + r
Sau năm thứ 3, cả gốc và lãi ông nhận được:
A 1 + r 2 + a 1 + r + a 1 + r = A 1 + r 3 + a 1 + r 2 + a 1 + r
…
Sau năm thứ n, ông Minh nhận được số tiền:
A 1 + r n + a 1 + r n − 1 + a 1 + r n − 2 + . .. + a = A 1 + r n + a . 1 + r n − 1 r
Thay số: sau 10 năm ông Minh nhận về cả gốc lẫn lãi là
200 1 + 0 , 07 10 + 20. 1 + 0 , 07 10 − 1 0 , 07 = 669 , 759 triệu đồng.

Đáp án A.


Gọi B là số tiền của người đó trong tài khoản tiết kiệm đến hết tháng 12 năm 2020. Khi đó n = 24
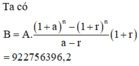
Đáp án A
Gọi u1là số tiền phải trả cho 10 số điện đầu tiên. u 1 = 10.800 = 8000 (đồng)
u2 là số tiền phải trả cho các số điện từ 11 đến 20: u 2 = u 1 1 + 0 , 025
u3 là số tiền phải trả cho các số điện từ 331 đến 340: u 34 = u 1 1 + 0.025 33
Số tiền phải trả cho 340 số điện đầu tiên là: S 1 = u 1 = 1 − 1 + 0 , 025 34 1 − 1 + 0 , 025 = 420903 , 08
Số tiền phải trả cho các số điện từ 341 đến 347 là: S 2 = 7.800 1 + 0 , 025 34 = 12965 , 80
Vậy tháng 1 gia đình ông A phải trả số tiền là: S = S 1 + S 2 = 433868 , 89 đồng.