Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
+ Điều kiện có sóng dừng trên dây với một đầu cố định và một đầu tự do
 .
.

Tần số nhỏ nhất để tạo thành sóng dừng trong trường hợp 1 đầu cố định, 1 đầu tự do là trên dây có nửa bó sóng:
\(\ell=\dfrac{\lambda}{4}=\dfrac{v}{4f_0}\Rightarrow f_0=\dfrac{v}{4\ell}=4Hz\) (ứng với 1 nút sóng)
Các tần số xảy ra sóng dừng là số lẻ lần \(f_0\): \(f_n=(2n+1).4\), số nút sóng là lẻ thì n cũng là số lẻ.
\(\Rightarrow n=2k+1\)
\(\Rightarrow f =[2.(2k+1)+1].4=(4k+3).4\)
Ta có: \(19\le(4k+3).4\le 80\Rightarrow 0,43\le k\le 4,25\)
Vậy các giá trí k thỏa mãn là: 1; 2; 3; 4
Do vậy, có 4 lần xảy ra sóng dừng.
\(f=\frac{\left(k+\frac{1}{2}\right)\upsilon}{2l}\)
Số lẻ thì không phải chẵn
\(19\le f=8\left(k+\frac{1}{2}\right)\le80\rightarrow k=2,4,6,8\)
Vậy có 4 lần

Đáp án B
*Trên một sợi dây đàn hồi hai đầu cố định có sóng dừng với bước sóng l . Chiều dài l của dây phải là số nguyên lần nữa bước sóng tức là
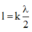 với k=1,2,3,….
với k=1,2,3,….

Chọn đáp án A
Dây đàn một đầu cố định, một đầu tự do, để có sóng dừng trên dây thì:
L = k . λ 2 + λ 4 = 2 k + 1 λ 4 = 2 k + 1 v 4 f ⇒ f = 2 k + 1 v 4 L
⇒ f min = v 4 L k h i k = 1
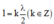
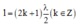
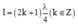
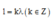
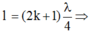
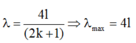
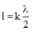
Chọn D
Để có sóng dừng xảy ra trên một sợi dây đàn hồi với hai đầu dây có một đầu cố định và một đầu tự do thì
l = k + 1 2 λ 2 = k λ 2 + λ 4