Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn B
Gọi x; y lần lượt là số cái bánh đậu xanh, bánh dẻo . Khi đó; số tiền lãi là L= 2x+ 1,8 y
Bài toán trở thành tìm số tự nhiên x; y thoả mãn hệ
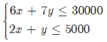 sao cho L= 2x+ 1,8 y lớn nhất.
sao cho L= 2x+ 1,8 y lớn nhất.
Từ đó ta có 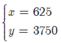 thì L đạt giá trị lớn nhất.
thì L đạt giá trị lớn nhất.
Vậy cần 625 bánh đậu xanh và 3750 bánh dẻo thì lãi lớn nhất.

Mỗi cách xếp 10 bức tranh thành một hàng ngang là một hoán vị của 10.
Số cách để họa sĩ sắp xếp các bức tranh là 10! = 3 628 800

Hình vuông có 3 cách tô
Hiình tròn có 2 cách tô
=> 3x2=6 cách tô
Hình vuông có 3 cách tô
Hiình tròn có 2 cách tô
=> 3x2=6 cách tô

Để chắc chắn lấy ra được ba bóng màu đỏ chúng ra cần xem xét khả năng xấu nhất chưa lấy ra được ba bóng màu đỏ: Toàn bộ bóng xanh và bóng vàng được lấy ra, do đó bắt buộc phải thêm 3 bóng đỏ nữa, và câu trả lời là cần lấy ra 28 bóng (28 = 15 + 10 + 3) thì chắc chắn có 3 bóng đỏ.
Đầu tiên phải lấy tổng số bóng xanh và bóng vàng ra
=> Cần phải lấy \(15+10=25\left(q\right)\)
Sau đó chỉ cần lấy thêm 3 quả nữa là chắc chắn có 3 quả mầu đỏ
=> Cần phải lấy \(25+3=28\left(q\right)\)

Các kết quả có thể của kiểu gen ứng với màu hạt của cây con là 4 nhánh cây \(AA,{\rm{A}}a,aA,Aa\).
Các kết quả có thể của kiểu gen ứng với dạng hạt của cây con là 4 nhánh cây \(BB,Bb,bB,bb\).
Vậy theo quy tắc nhân, số phần tử của không gian mẫu là \(n\left( \Omega \right) = 4.4 = 16\).
Gọi \(E\) là biến cố: “Cây con có hạt màu vàng và trơn”.
Cây con có hạt màu vàng và trơn khi và chỉ khi trong kiểu gen màu hạt có ít nhất một gen trội A và trong kiểu gen hình dạng hạt có ít nhất một gen trội B. Do đó \(E=\{(AA,BB);\)\((AA,Bb); \)\( (AA,bB); \)\( (Aa,BB); \)\( (Aa;Bb); \)\( (Aa;bB); \)\( (aA;BB); \)\( (aA;Bb); \)\( (aA;bB)\}\).
Vậy \(P\left( E \right) = \frac{9}{{16}}\).

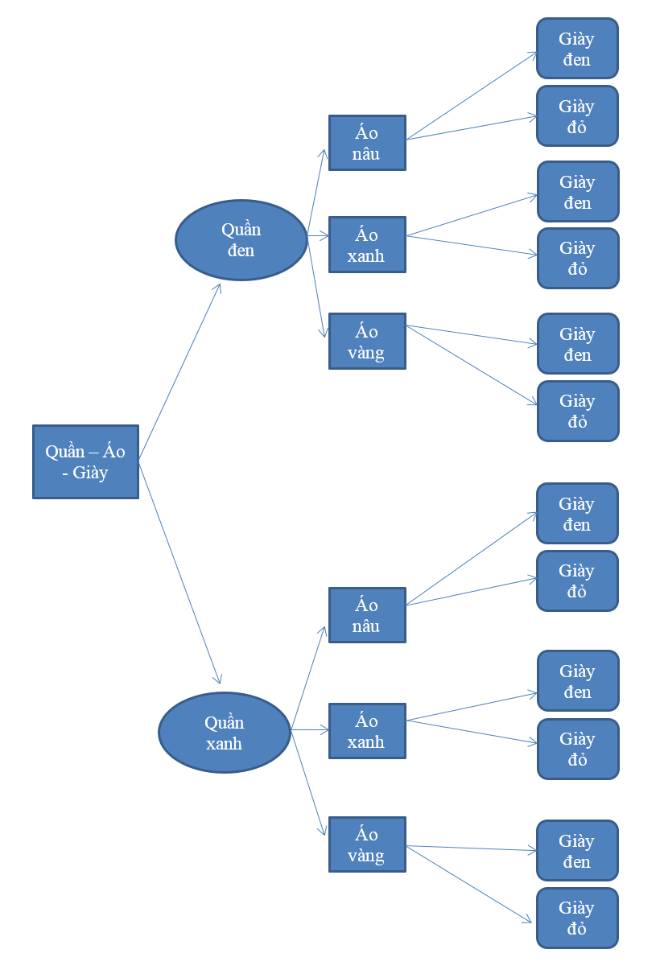
Kết luận: Từ sơ đồ cây, ta thấy bạn Dương có 12 cách chọn một bộ quần áo và một đôi giày.
Gọi \(x\) là tranh loại 1,2 màu đỏ có thể làm được
Gọi
 là tranh loại 1,2 màu xanh có thể làm được
là tranh loại 1,2 màu xanh có thể làm được
Gọi \(z\) là tranh loại 1,2 màu vàng có thể làm được
\(BCNN\left(4;6\right)=12\)
\(\Rightarrow x\in BC\left(12\right)=\left\{12;24;36;...;192;204;...\right\}\)
mà \(0< x\le200\)
\(\Rightarrow x=192\left(1\right)\)
\(BCNN\left(0,5;0,75\right)=0,75\)
\(\Rightarrow y\in BC\left(0,75\right)=\left\{0,75;1,5;...;19,5;20,25;...\right\}\)
mà \(0< y\le20\)
\(\Rightarrow y=20\left(y\in N\right)\left(2\right)\)
\(BCNN\left(1;1,5\right)=1,5\)
\(\Rightarrow y\in BC\left(1,5\right)=\left\{1,5;3;...49,5;51\right\}\)
mà \(0< z\le50\)
\(\Rightarrow z=50\left(z\in N\right)\left(3\right)\)
\(\left(1\right);\left(2\right);\left(3\right)\) ta được tổng số tranh lớn nhất của loại 1,2 là 20 bức tranh
hay \(a+b=20\)
Số tiền bức tranh 1 là : \(20000a\)
Số tiền bức tranh 2 là : \(50000b\)
Vậy để mỗi loại thu được số tiền nhiều nhất
\(\Rightarrow a=b=10\)
Vậy cần phải làm tranh loại 1 : 10 bức tranh;
loại 2 : 10 bức tranh