B
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
3 tháng 4 2017
a) 2cos2x - 3cosx + 1 = 0 (1)
Đặt : t = cosx với điều kiện -1 \(\le t\le1\)
(1)\(\Leftrightarrow\) 2t2 - 3t + 1= 0
\(\Leftrightarrow\left[{}\begin{matrix}t=1\\t=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=\dfrac{1}{2}=cosx\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\left(k\in Z\right)}\)
BT
22 tháng 5 2017
a) Đkxđ: D = R
Đặt \(cosx=t;\left|t\right|\le1\). Phương trình trở thành:m\(2t^2-3t+1=0\Leftrightarrow\left[{}\begin{matrix}t=1\left(tm\right)\\t=\dfrac{1}{2}\left(tm\right)\end{matrix}\right.\).
Với \(t=1\) ta có \(cosx=1\)\(\Leftrightarrow x=k2\pi\).
Với \(t=\dfrac{1}{2}\) ta có \(cosx=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\).
Vậy phương trình có 3 họ nghiệm là:
- \(x=k2\pi\);
- \(x=\dfrac{\pi}{3}+k2\pi\);
- \(x=-\dfrac{\pi}{3}+k2\pi\).
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 7 2020
a/ \(cos\left(2x+\frac{\pi}{6}\right)=0\)
\(\Leftrightarrow2x+\frac{\pi}{6}=\frac{\pi}{2}+k\pi\)
\(\Rightarrow x=\frac{\pi}{6}+\frac{k\pi}{2}\)
b/ \(cos\left(4x-\frac{\pi}{3}\right)=1\)
\(\Leftrightarrow4x-\frac{\pi}{3}=k2\pi\)
\(\Rightarrow x=\frac{\pi}{12}+\frac{k\pi}{2}\)
c/ \(cos\left(2x+25^0\right)=-\frac{\sqrt{2}}{2}=cos135^0\)
\(\Rightarrow\left[{}\begin{matrix}2x+25^0=135^0+k360^0\\2x+25^0=-135^0+k360^0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=55^0+k180^0\\x=-80^0+k180^0\end{matrix}\right.\)
d/ \(cot\left(3x+10^0\right)=\frac{\sqrt{3}}{3}=cot60^0\)
\(\Rightarrow3x+10^0=60^0+k180^0\)
\(\Rightarrow x=\frac{50^0}{3}+k60^0\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 6 2020
16.
\(y'=\frac{\left(cos2x\right)'}{2\sqrt{cos2x}}=\frac{-2sin2x}{2\sqrt{cos2x}}=-\frac{sin2x}{\sqrt{cos2x}}\)
17.
\(y'=4x^3-\frac{1}{x^2}-\frac{1}{2\sqrt{x}}\)
18.
\(y'=3x^2-2x\)
\(y'\left(-2\right)=16;y\left(-2\right)=-12\)
Pttt: \(y=16\left(x+2\right)-12\Leftrightarrow y=16x+20\)
19.
\(y'=-\frac{1}{x^2}=-x^{-2}\)
\(y''=2x^{-3}=\frac{2}{x^3}\)
20.
\(\left(cotx\right)'=-\frac{1}{sin^2x}\)
21.
\(y'=1+\frac{4}{x^2}=\frac{x^2+4}{x^2}\)
22.
\(lim\left(3^n\right)=+\infty\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 6 2020
11.
\(\lim\limits_{x\rightarrow1^+}\frac{-2x+1}{x-1}=\frac{-1}{0}=-\infty\)
12.
\(y=cotx\Rightarrow y'=-\frac{1}{sin^2x}\)
13.
\(y'=2020\left(x^3-2x^2\right)^{2019}.\left(x^3-2x^2\right)'=2020\left(x^3-2x^2\right)^{2019}\left(3x^2-4x\right)\)
14.
\(y'=\frac{\left(4x^2+3x+1\right)'}{2\sqrt{4x^2+3x+1}}=\frac{8x+3}{2\sqrt{4x^2+3x+1}}\)
15.
\(y'=4\left(x-5\right)^3\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 9 2020
\(sina+sinb+sinc+3=0\)
\(\Leftrightarrow\left(sina+1\right)+\left(sinb+1\right)+\left(sinc+1\right)=0\)
Do \(\left\{{}\begin{matrix}sina\ge-1\\sinb\ge-1\\sinc\ge-1\end{matrix}\right.\) ;\(\forall a;b;c\)
\(\Rightarrow\left(sina+1\right)+\left(sinb+1\right)+\left(sinc+1\right)\ge0\)
Dấu "=" xảy ra khi và chỉ khi \(sina=sinb=sinc=-1\)
\(\Rightarrow cosa=cosb=cosc=0\Rightarrow cosa+cosb+cosc+10=10\)
b/ \(sinx=1-sin^2x\Rightarrow sinx=cos^2x\)
\(\Rightarrow sin^2x=cos^4x\Rightarrow1-cos^2x=cos^4x\)
\(\Rightarrow cos^4x+cos^2x=1\Rightarrow\left(cos^4x+cos^2x\right)^2=1\)
\(\Rightarrow cos^8x+2cos^6x+cos^4x=1\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 6 2020
1/ a/ \(y'=-5sinx+\frac{3}{cos^2\left(x+15^0\right)}\)
b/ \(y'=\frac{6cos3x\left(-4cosx-5\right)-8sinx.sin3x}{\left(4cosx+5\right)^2}\)
2/ \(y'=-3cosx-\frac{15}{sin^23x}\Rightarrow y'\left(\frac{\pi}{4}\right)=-3cos\left(\frac{\pi}{4}\right)-\frac{15}{sin^2\left(\frac{3\pi}{4}\right)}=-\frac{60+3\sqrt{2}}{2}\)
3/ \(y'=4x-5\)
a/ \(y'\left(2\right)=3\) ; \(y\left(2\right)=2\)
Tiếp tuyến: \(y=3\left(x-2\right)+2=3x-4\)
b/ Tiếp tuyến song song \(y=2x-3\Rightarrow\) có hệ số góc bằng 2
\(\Rightarrow4x_0-5=2\Rightarrow x_0=\frac{7}{4}\Rightarrow y\left(\frac{7}{4}\right)=\frac{11}{8}\)
Tiếp tuyến: \(y=2\left(x-\frac{7}{4}\right)+\frac{11}{8}\)
c/ \(-x+3y-1=0\Rightarrow y=\frac{1}{3}x+\frac{1}{3}\)
Tiếp tuyến vuông góc với d nên có hệ số góc bằng \(-3\)
\(\Rightarrow4x_0-5=-3\Rightarrow x_0=\frac{1}{2}\Rightarrow y\left(\frac{1}{2}\right)=2\)
Tiếp tuyến: \(y=-3\left(x-\frac{1}{2}\right)+2\)
5 tháng 6 2020
3/ a, y=\(2x^2-5x+4\)
Ta có: \(x_o=2\)-> \(y_0=2\)
-> \(f'\left(x_0\right)=3\)
Nên ta có pttt: y'= 3x - 4
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 6 2020
25.
H là hình chiếu của S lên (ABC)
Do \(SA=SB=SC\Rightarrow HA=HB=HC\)
\(\Rightarrow\) H là tâm đường tròn ngoại tiếp tam giác ABC
26.
\(\left\{{}\begin{matrix}AB\perp BC\\AB\perp CD\end{matrix}\right.\) \(\Rightarrow AB\perp\left(BCD\right)\) \(\Rightarrow AB\perp BD\)
\(\Rightarrow\Delta ABD\) vuông tại B
Pitago tam giác vuông BCD (vuông tại C):
\(BC^2+CD^2=BD^2\Rightarrow BD^2=b^2+c^2\)
Pitago tam giác vuông ABD:
\(AD^2=AB^2+BC^2=a^2+b^2+c^2\)
\(\Rightarrow AD=\sqrt{a^2+b^2+c^2}\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 6 2020
23.
Gọi H là chân đường cao hạ từ S xuống BC
\(\Rightarrow BH=SB.cos30^0=3a\) ; \(SH=SB.sin30^0=a\sqrt{3}\) ; \(CH=4a-3a=a\)
\(\Rightarrow BC=4HC\Rightarrow d\left(B;\left(SAC\right)\right)=4d\left(H;\left(SAC\right)\right)\)
Từ H kẻ \(HE\perp AC\) ; từ H kẻ \(HF\perp SE\Rightarrow HF\perp\left(SAC\right)\)
\(\Rightarrow HF=d\left(H;\left(SAC\right)\right)\)
\(HE=CH.sinC=\frac{CH.AB}{AC}=\frac{a.3a}{5a}=\frac{3a}{5}\)
\(\frac{1}{HF^2}=\frac{1}{HE^2}+\frac{1}{SH^2}\Rightarrow HF=\frac{HE.SH}{\sqrt{HE^2+SH^2}}=\frac{3a\sqrt{7}}{14}\)
\(\Rightarrow d\left(B;\left(SAC\right)\right)=4HF=\frac{6a\sqrt{7}}{7}\)
24.
\(SA=SC\Rightarrow SO\perp AC\)
\(SB=SD\Rightarrow SO\perp BD\)
\(\Rightarrow SO\perp\left(ABCD\right)\)
MH
9 tháng 4 2017
a) Dễ thấy cosx = 0 không thỏa mãn phương trình đã cho nên chiaw phương trình cho cos2x ta được phương trình tương đương 2tan2x + tanx - 3 = 0.
Đặt t = tanx thì phương trình này trở thành
2t2 + t - 3 = 0 ⇔ t ∈ {1 ; 
}.
Vậy 
b) Thay 2 = 2(sin2x + cos2x), phương trình đã cho trở thành
3sin2x - 4sinxcosx + 5cos2x = 2sin2x + 2cos2x
⇔ sin2x - 4sinxcosx + 3cos2x = 0
⇔ tan2x - 4tanx + 3 = 0
⇔ 
⇔ x = 
+ kπ ; x = arctan3 + kπ, k ∈ Z.
c) Thay sin2x = 2sinxcosx ; 
= (sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
sin2x + 2sinxcosx - 
cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔ 
⇔ x = + kπ ; x = arctan(-5) + kπ, k ∈ Z.
d) 2cos2x - 3√3sin2x - 4sin2x = -4
⇔ 2cos2x - 3√3sin2x + 4 - 4sin2x = 0
⇔ 6cos2x - 6√3sinxcosx = 0 ⇔ cosx(cosx - √3sinx) = 0
⇔ 
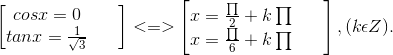
\(3^{2x}=\left(3^x\right)^2=5^2=25\) -> D