K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
T
22 tháng 12 2023
a) ĐKXĐ: \(x\ne0;x\ne-2\)
b) \(S=\dfrac{\left(x+2\right)^2}{x}\cdot\left(1-\dfrac{x^2}{x+2}\right)-\dfrac{x^2+6x+4}{x}\)
\(=\dfrac{\left(x+2\right)^2}{x}\cdot\dfrac{x+2-x^2}{x+2}-\dfrac{x^2+6x+4}{x}\)
\(=\dfrac{\left(x+2\right)\left(x+2-x^2\right)}{x}-\dfrac{x^2+6x+4}{x}\)
\(=\dfrac{x^2+2x-x^3+2x+4-2x^2-x^2-6x-4}{x}\)
\(=\dfrac{-x^3-2x^2-2x}{x}\)
\(=\dfrac{x\left(-x^2-2x-2\right)}{x}\)
\(=-x^2-2x-2\)
Với \(x=0\Rightarrow\) loại
Với \(x=1\), thay vào \(S\) ta được
\(S=-1^2-2\cdot1-2=-5\)
c) Có: \(S=-x^2-2x-2\)
\(=-\left(x^2+2x+2\right)\)
\(=-\left(x^2+2x+1\right)-1\)
\(=-\left(x+1\right)^2-1\)
Ta thấy: \(\left(x+1\right)^2\ge0\forall x\ne0;x\ne-2\)
\(\Rightarrow-\left(x+1\right)^2\le0\forall x\ne0;x\ne-2\)
\(\Rightarrow S=-\left(x+1\right)^2-1\le-1\forall x\ne0;x\ne-2\)
Dấu \("="\) xảy ra khi: \(x+1=0\Leftrightarrow x=-1\left(tmdk\right)\)
\(\text{#}\mathit{Toru}\)
HH
2
8 tháng 9 2020
\(3\left(2a-1\right)+5\left(3-a\right)\)
\(=6a-3+15-5a\)
\(=a+12\)
8 tháng 9 2020
3( 2a - 1 ) + 5( 3 - a )
= 6a - 3 + 15 - 5a
= a + 12
Rồi a bằng bao nhiêu thì bạn thay vào
#Good luck :)
19 tháng 8 2023
\(A=\dfrac{4x+8-3x+6}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x^2}{x+14}\)
\(=\dfrac{x+14}{x+14}\cdot\dfrac{x^2}{x^2-4}=\dfrac{x^2}{x^2-4}\)
Khi x=-3 thì \(A=\dfrac{\left(-3\right)^2}{\left(-3\right)^2-4}=\dfrac{9}{5}\)
17 tháng 4 2021
\(\dfrac{8-2x}{x^2+x-20}=-\dfrac{2\left(4-x\right)}{\left(4-x\right)\left(x+5\right)}=\dfrac{-2}{x+5}\)
Để biểu thức trên nhận giá trị dương khi
\(x+5< 0\)do -2 < 0
\(\Leftrightarrow x< -5\)
H9
HT.Phong (9A5)
CTVHS
14 tháng 8 2023
\(P=\dfrac{x^2-1}{x+5}\cdot\dfrac{2x+10}{x^2-x}\) (ĐK: \(x\ne-1,x\ne0,x\ne1\))
\(P=\dfrac{\left(x-1\right)\left(x+1\right)}{x+5}\cdot\dfrac{2\left(x+5\right)}{x\left(x-1\right)}\)
\(P=\dfrac{2\left(x-1\right)\left(x+1\right)\left(x+5\right)}{x\left(x+5\right)\left(x-1\right)}\)
\(P=\dfrac{2\left(x+1\right)}{x}\)
Thay \(x=99\left(tm\right)\) vào P ta có:
\(P=\dfrac{2\left(99+1\right)}{99}=\dfrac{2\cdot100}{99}=\dfrac{200}{99}\)
14 tháng 8 2023
\(P=\dfrac{x^2-1}{x+5}\cdot\dfrac{2x+10}{x^2-x}\\ =\dfrac{\left(x^2-1\right)\left(2x+10\right)}{\left(x+5\right)\left(x^2-x\right)}\\ =\dfrac{\left(x+1\right)\left(x-1\right)\left(x+5\right)2}{\left(x+5\right)\left(x-1\right)x}\\ =\dfrac{2x+2}{x}\)
Thay \(x=99\) vào P ta có
\(P=\dfrac{2.99+2}{99}\\ =\dfrac{200}{99}\)
Vậy \(x=99\) thì \(P=\)\(\dfrac{200}{99}\)
26 tháng 12 2021
a)(x-10)2-x(x+80)
(x2-2x10+100)-x2-80x
=x2-20x+100-x2-80x=-100x+100
khi x = 0.98
ta có
(-100*0.98)+100=-98+100=2
b)x3-9x+27x-27
hình như là -27x :))
DT
.
1
26 tháng 5 2022
Tham khảo:
* Rút gọn biểu thức:
+ Ngoặc thứ nhất:
+ Ngoặc thứ hai:
Do đó:
* Tại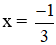 
, giá trị biểu thức bằng: 
11 tháng 12 2023
d: \(D=x^3-6x^2+12x-100\)
\(=x^3-6x^2+12x-8-92\)
\(=\left(x-2\right)^3-92\)
Khi x=-98 thì \(D=\left(-98-2\right)^3-92=-1000000-92=-1000092\)
e: \(E=\left(x+1\right)^3+6\left(x+1\right)^2+12x+20\)
\(=\left(x+1\right)^3+6\left(x+1\right)^2+12\left(x+1\right)+8\)
\(=\left(x+1+2\right)^3\)
\(=\left(x+3\right)^3\)
Khi x=5 thì \(E=\left(5+3\right)^3=8^3=512\)
f: \(F=\left(2x-1\right)\left(4x^2+2x+1\right)-7\left(x^3+1\right)\)
\(=\left(2x\right)^3-1^3-7x^3-7\)
\(=x^3-8\)
Khi x=-1/2 thì \(F=\left(-\dfrac{1}{2}\right)^3-8=-\dfrac{1}{8}-8=-\dfrac{65}{8}\)
g: \(G=\left(-x-2\right)^3+\left(2x-4\right)\left(x^2+2x+4\right)-x^2\left(x-6\right)\)
\(=-\left(x+2\right)^3+2\left(x-2\right)\left(x^2+2x+4\right)-x^3+6x^2\)
\(=-x^3-6x^2-12x-8+2\left(x^3-8\right)-x^3+6x^2\)
\(=-2x^3-12x-8+2x^3-16=-12x-24\)
Khi x=-2 thì \(G=-12\cdot\left(-2\right)-24=24-24=0\)
h: \(H=\left(x-1\right)^3-\left(x+2\right)\left(x^2-2x+4\right)+3\left(x+4\right)\left(x-4\right)\)
\(=x^3-3x^2+3x-1-\left(x^3+8\right)+3\left(x^2-16\right)\)
\(=x^3-3x^2+3x-1-x^3-8+3x^2-48\)
\(=3x-57\)
Khi x=-1/2 thì \(H=3\cdot\dfrac{-1}{2}-57=-1,5-57=-58,5\)
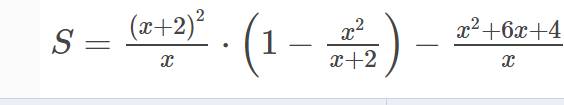
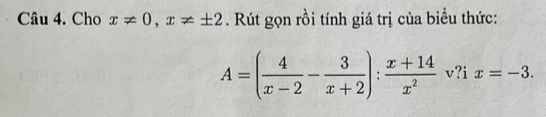
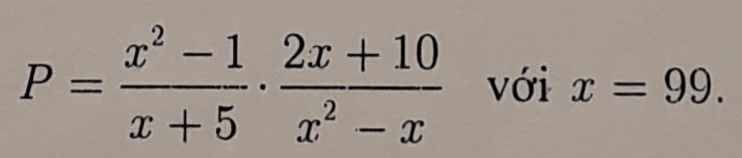
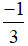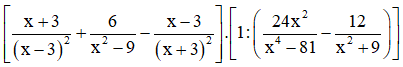
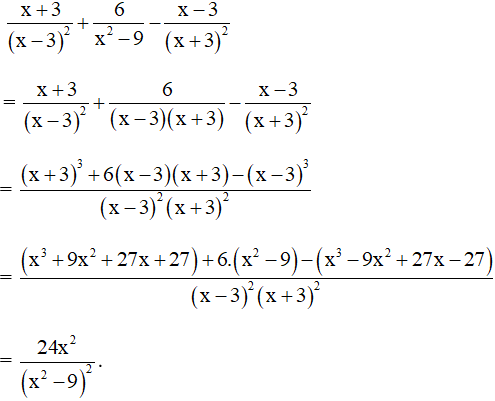
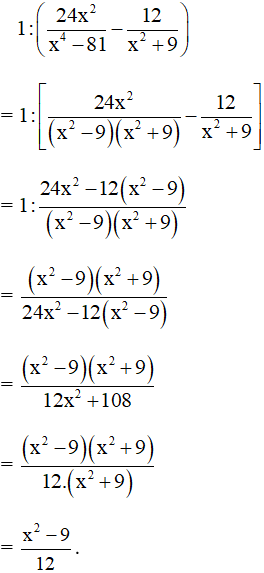
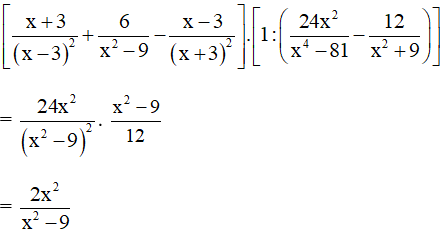
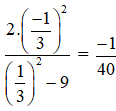
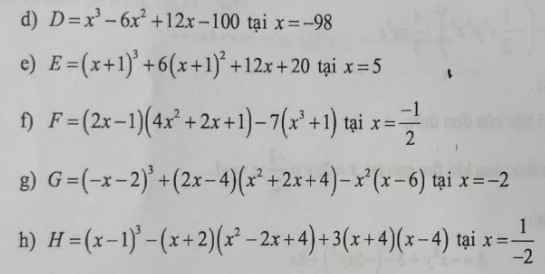
c) Ta có: \(C=7\left(x-8\right)^2-9\left(x+3\right)^2+50\)
\(=7\left(x^2-16x+64\right)-9\left(x^2+6x+9\right)+50\)
\(=7x^2-112x+448-9x^2-54x-81+50\)
\(=-2x^2-166x-31\)
\(=-2\cdot\dfrac{1}{49}-166\cdot\dfrac{-1}{7}-31\)
\(=\dfrac{-359}{49}\)
g) Ta có: \(G=x^{17}-3x^{16}+3x^{15}-3x^{14}+...+3x\)
\(=x^{17}-x^{16}\left(x+1\right)+x^{15}\left(x+1\right)-x^{14}\left(x+1\right)+...+x\left(x+1\right)\)
\(=x^{17}-x^{17}-x^{16}+x^{16}+x^{15}-x^{15}-x^{14}+...+x^2+x\)
=x
=2