Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

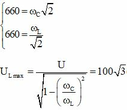
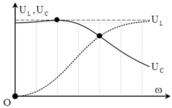
Từ đồ thị, ta thấy rằng ω R = 2 ω C → n = 4.
Áp dụng công thức chuẩn hóa .
U L m a x = U 1 − n − 2 ⇒ U L m a x U = 1 1 − n − 2 = 1 , 03
Đáp án C

Từ đồ thị, ta thấy rằng ω R = 2 ω C → n = 4.
Áp dụng công thức chuẩn hóa U L m a x = U 1 − n − 2 ⇒ U L m a x U = 1 1 − n − 2 = 1 , 03 .
Đáp án C

Đáp án C
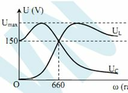
Ta có ngay U = 150 (V) ( ω = 0 thì U C = U)
Gọi ω C là giá trị để U C max, ω L là giá trị để U C max. Ta có

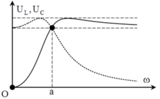
Khi tần số góc ω biến thiên thì thứ tự xuất hiện cực đại của điện áp hiệu dụng trên các phần tử là U C , U R v à U L .
→ (1) cực đại đầu tiên → (1) là U C .
→ (2) cực đại tiếp theo → (2) là U R → (3) là U L .
Đáp án A

Điện áp hiệu dụng hai đầu cuộn cảm theo tần số góc ω được cho bởi biểu thức:
U L = U Z L R 2 + Z L − Z C 2 = U 1 C 2 L 2 1 ω 4 + R 2 L 2 − 2 L C 1 ω 2 + 1 ⇒ 1 C 2 L 2 1 ω 4 + R 2 L 2 − 2 L C 1 ω 2 + 1 − U U L 2 = 0
Với hai giá trị của tần số cho cùng một điện áp hiệu dụng trên cuộn cảm, ta luôn có:
1 ω 1 2 1 ω 2 2 = 1 − U U L 2 1 L 2 C 2 ⇔ ω 0 4 ω 1 2 ω 2 2 = 1 − U U L 2 = 1 − 4 5 2 = 0 , 36
Đáp án B

Điện áp hiệu dụng hai đầu cuộn cảm theo tần số góc ω được cho bởi biểu thức:
U L = U Z L R 2 + Z L − Z C 2 = U 1 C 2 L 2 1 ω 4 + R 2 L 2 − 2 L C 1 ω 2 + 1
→ 1 C 2 L 2 1 ω 4 + R 2 L 2 − 2 L C 1 ω 2 + 1 − U U L 2 = 0
Với hai giá trị của tần số cho cùng một điện áp hiệu dụng trên cuộn cảm, ta luôn có:
1 ω 1 2 1 ω 2 2 = 1 − U U L 2 1 L 2 C 2 ⇔ ω 0 4 ω 1 2 ω 2 2 = 1 − U U L 2 = 1 − 4 5 2 = 0 , 36
Đáp án B

Khi ω = ω 0 → mạch xảy ra cộng hưởng → điện áp hiệu dụng trên điện trở là cực đại → A đúng → B sai.
Đáp án B
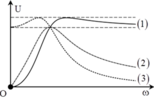
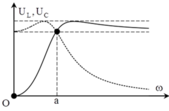


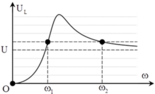
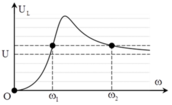
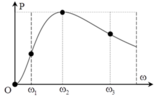
Thứ tự các đồ thị sẽ là: U C – ( 3 ) , U L – ( 1 ) v à U R – ( 2 ) .
Đáp án B