Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhận xét: \(200^2=100^2+\left(100\sqrt{3}\right)^2\)
Nên u vuông pha với ud như hình vẽ.
\(\Rightarrow\varphi_d=\varphi_u+\frac{\pi}{2}=\frac{\pi}{4}+\frac{\pi}{2}=\frac{3\pi}{4}\)
Biểu thức điện áp hai đầu cuộn dây: \(u=100\sqrt{2}\cos\left(100\pi t+\frac{3\pi}{4}\right)\)

Bạn nên gửi mỗi câu hỏi một bài thôi để mọi người tiện trao đổi.
1. \(Z_L=200\sqrt{3}\Omega\), \(Z_C=100\sqrt{3}\Omega\)
Suy ra biểu thức của i: \(i=1,1\sqrt{2}\cos\left(100\pi t-\frac{\pi}{3}\right)A\)
Công suất tức thời: p = u.i
Để điện áp sinh công dương thì p > 0, suy ra u và i cùng dấu.
Biểu diễn vị trí tương đối của u và i bằng véc tơ quay ta có:
Như vậy, trong 1 chu kì, để u, i cùng dấu thì véc tơ u phải quét 2 góc như hình vẽ.
Tổng góc quét: 2.120 = 2400
Thời gian: \(t=\frac{240}{360}.T=\frac{2}{3}.\frac{2\pi}{100\pi}=\frac{1}{75}s\)
2. Khi nối tắt 2 đầu tụ điện thì cường độ dòng điện hiệu dụng không đổi \(\Rightarrow Z_1=Z_2\Leftrightarrow Z_C-Z_L=Z_L\Leftrightarrow Z_C=2Z_L\)
\(U_C=1,2U_d\Leftrightarrow Z_C=2Z_d\Leftrightarrow Z_C=2\sqrt{R^2+Z_L^2}\)
\(\Leftrightarrow2Z_L=\sqrt{R^2+Z_L^2}\Leftrightarrow R=\sqrt{3}Z_L\)
Khi bỏ tụ C thì cường độ dòng điện của mạch là: \(I=\frac{U}{Z_d}=\frac{U}{\sqrt{R^2+Z_L^2}}=\frac{220}{\sqrt{3.Z_L^2+Z_L^2}}=0,5\)
\(\Rightarrow Z_L=220\Omega\)

Giải thích: Đáp án C
Tính điện áp giữa hai đầu điện trở: 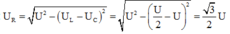
Hệ số công suất của đoạn mạch: 

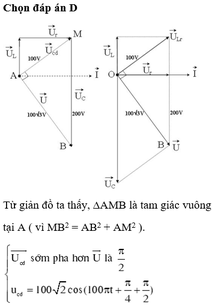
Đáp án D
Phương pháp: Sử dụng giản đồ vecto
Cách giải:
Vì điện áp hai đầu cuộn dây sớm pha π/2 so với điện áp hai đầu mạch nên trong cuộn dây có điện trở r
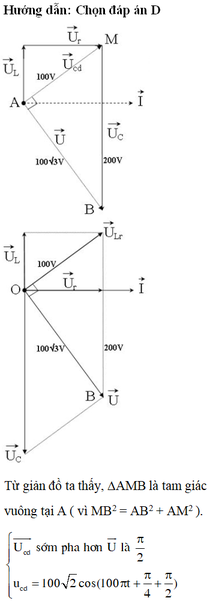
Vì điện áp hiệu dụng của cuộn dây bằng điện áp hiệu dụng đặt vào 2 đầu mạch, lại lệch pha nhau π/2, dựa vào hình vẽ ta thấy tam giác ABO là tam giác vuông cân.
Tức là
![]()
![]()

Đo điện áp giữa hai đầu tụ điện và 2 đầu điện trở số chỉ vôn kế như nhau
\(\Rightarrow U_C=U_R\)
\(Z_L=2Z_C\Rightarrow U_L=2U_C\)
\(\tan\varphi=\frac{U_L-U_C}{U_R}=\frac{2U_C-U_C}{U_C}=1\)
\(\Rightarrow\varphi=\frac{\pi}{4}\)
Như vậy điện áp 2 đầu đoạn mạch lệch pha \(\frac{\pi}{4}\)so với dòng điện
Chọn A.

+ \(U_{AM}=I.Z_{AM}\), \(Z_{AM}\)không thay đổi, nên để \(U_{AM}\) đạt giá trị lớn nhất khi thay đổi C thì dòng điện Imax --> Xảy ra hiện tượng cộng hưởng: \(Z_L=Z_C\)
và \(I=\frac{U}{R+r}\)
Công suất của cuộn dây khi đó: \(P=I^2.r=\left(\frac{U}{R+r}\right)^2.r\) (*)
+ Nếu đặt vào 2 đầu AB một điện áp không đổi và nối tắt tụ C thì mạch chỉ gồm r nối tiếp với R (L không có tác dụng gì)
Cường độ dòng điện của mạch: \(I=\frac{25}{R+r}=0,5\Rightarrow R+r=50\)
Mà R = 40 suy ra r = 10.
Thay vào (*) ta đc \(P=\left(\frac{200}{50}\right)^2.10=160W\)
Bạn học đến điện xoay chiều rồi à. Học nhanh vậy, mình vẫn đang ở dao động cơ :(
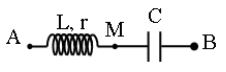
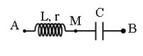
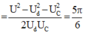
Theo đề bài thì cuộn dây không thuần cảm, có điện trở r.
Ta có:
\(\begin{cases} U=100\sqrt{3} \\ U_d=100 \\ U_C=200 \end{cases} \Rightarrow \begin{cases} U_r^2+\left(U_L-U_C\right)^2=3.100^2 \\ U_r^2+U_L^2 =100^2 \\ U_C^2=200 \end{cases}\)
\(\Rightarrow U_r=50\sqrt{3}, U_L=50, U_C=200\)
\(\Rightarrow \tan \varphi = \dfrac{Z_L-Z_C}{r}=-\sqrt{3} , \tan \varphi_d=\dfrac{Z_L}{r} =\dfrac{1}{\sqrt{3}} \Rightarrow u_d \perp u\)
\(\Rightarrow u_d=100\sqrt{2}\cos \left(100\pi t +\dfrac{3\pi }{4}\right)\) (V)