Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1: ta có hình vẽ sau: \(SI\) là tia tới
\(SI\) là tia tới
\(IR\) là tia phản xạ
\(\Rightarrow\) \(IR=SI=32^o\) (góc phản xạ)
\(\Rightarrow IR+SI=32^o+32^o=62^o\) (góc hợp bởi tia tới và tia phản xạ)
Câu 2: ta có hình vẽ sau:

\(FI\) là tia tới
\(IR\) là tia phản xạ
\(\Rightarrow FI=\widehat{I}-40^o=90^o-40^o=50^0\) (góc tới)
\(\Rightarrow IR=FI=50^0\) (góc phản xạ)
\(\Rightarrow FI+IR=50^o+50^o=100^o\) (góc hợp bởi tia tới và tia phản xạ)
Câu 3: ta có hình vẽ sau: (hình vẽ hợi xấu + không được đúng cho lắm)


Vẽ hình:
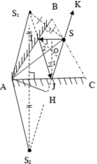
a) S1 là ảnh của S qua gương AB => S1 đối xứng với S qua AB
S2 là ảnh của S1 qua gương AC => S2 đối xứng với S 1 qua AC
Ta nối S2 với S cắt AC tại J, nối J với S1 cắt AB tại I
=> SI, IJ, JS là ba đoạn của tia sáng cần dựng.
b) Dựng hai phỏp tuyến tại I và J cắt nhau tai O
Góc tạo bởi tia phản xạ JK và tia tới SI là ∠ ISK
Theo tính chất góc ngoài tam giác ta có
I S K ^ = I ^ + J ^ = 2 I ^ 2 + 2 J ^ 2 = 2 ( 180 0 − I O ^ J ) = 2. B A ^ C = 120 0
c) Tổng độ dài ba đoạn:
SI + IJ + JS = S1I + IJ + JS = S1J + JS = S2J + JS = S2S
(Đối xứng trục)
Vậy SI + IJ + JS = S2S
Ta có:
∠ S1AS = 2 ∠ S1AB (1)
∠ S1AS2 = 2 ∠ S1AC (2)
Lấy (2) – (1):
∠ S1AS2 - ∠ S1AS = 2( ∠ S1AC - ∠ S1AB)
ð ∠ SAS2 = 2 ∠ BAC
ð ∠ SAS2 = 1200
Xét tam giác cân SAS2 tại A, có ∠ A = 1200
ð ∠ ASH = ∠ AS2H = 300 với đường cao AH, ta có: SS2 = 2SH
Xét tam giác vuông SAH taị H có ∠ ASH = 300 ta có: AH = AS/2
Trong tam giác vuông SAH tại H.
Theo định lí pitago ta tính được SH= S A . 3 2
nên SS2 = 2SH = 2. S A . 3 2 = SA 3
=> SS2 nhỏ nhất ó SA nhỏ nhất ó AS là đường cao của tam giác đều ABC
ó S là trung điểm của BC.
mấy dòng cúi đọc chả hiểu j nhưng mình vẫn chép
thank you so much
I LOVE YOU chụt chụt...