Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

GIẢI THÍCH: Công suất tức thời tại thời điểm t:
p(t) = ui = I.√2cos(ωt).U√2cos(ωt + φ) = UIcosφ + UIcos(2ωt + φ) = UI.k + p1
⇒ vị trí cân bằng của p(t) tịnh tiến lên một khoảng UI.k
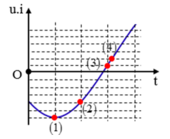
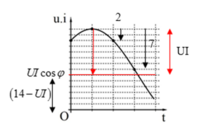
Chuẩn hóa 1 ô theo trục tung = 1. Đặt A = UI. Xét điểm (1), (2) và (3) trên đồ thị:
Thời gian từ (1): p(t) = -A đến (2): p(t) = -(A – 2) bằng khoảng t/g từ (2) đến (3) : p(t) = -(A – 7)
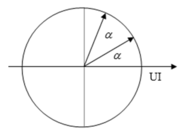
⇒ φ 1 = φ 2 = φ (biểu diễn trên đường tròn lượng giác)
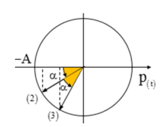

Chọn C.

Giải thích: Đáp án C
Phương pháp: Từ đồ thị viết phương trình của u và tính được chu kì T
Sử dụng đường tròn lượng giác
Cách giải: i=2cos(ωt – π 6 )A
+ Điện áp:
Từ đồ thị ta có:
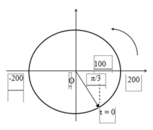
=> Pha ban đầu: φu = -π/3 (rad)
=> Phương trình của điện áp: 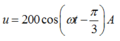
+ Tổng trở: 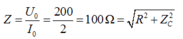
+ Độ lệch pha giữa u và i:

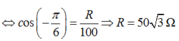

+ Từ đồ thị
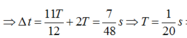
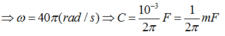

Đáp án C
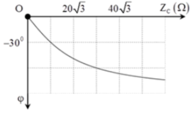
+ Mối liên hệ giữa φ và Z C : tan φ = Z C R
Từ đồ thị ta thấy, khi Z C = 10 3 thì φ = - 30 0 . Thay vào biểu thức trên, ta tìm được R = 30 Ω.
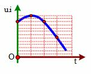
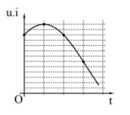
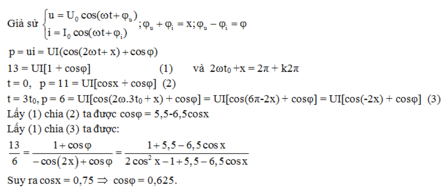
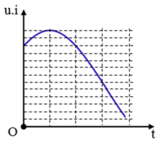
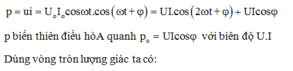
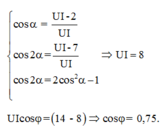

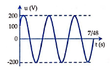

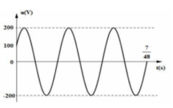
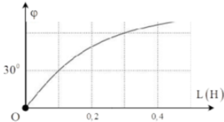
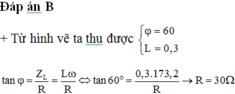
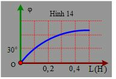
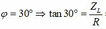
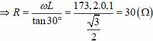
Chọn đáp án A
p = u i = U I ( cos ( 2 ω t + x ) + cos φ )
13 = UI[1 + cosφ] (1) và 2ωt0 +x = 2π + k2π
t = 0, p = 11 = UI[cosx +cosφ] (2)
t = 3 t 0 , p = 6 = UI[cos(2ω.3 t 0 +x) + cosφ]= UI[cos(6π−2x) + cosφ] = UI[cos(−2x) + cosφ] (3)
Lấy (1) chia (2) ta được cosφ = 5,5−6,5cosx
Lấy (1) chia (3) ta được 13/6= [ 1 + cosφ]/[−cos(2x) + cosφ]= [1+5,5−6,5cosx]/[2. cos 2 x −1 +5,5 −6,5cosx]
Suy ra cosx = 0,75 => cosφ = 0,625