Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ Khi xảy ra cực đại của điện áp hiệu dụng trên tụ thì uRL vuông pha với u.
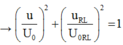
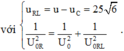
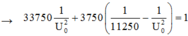
![]()

Đáp án A
+ Điện áp hiệu dụng trên tụ đ→ u vuông pha với uRL, khi 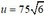
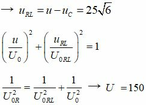

Đáp án: B
Sử dụng các công thức của bài toán điện dung của tụ điện thay đổi.
Điều chỉnh C để điện áp hiệu dụng hai đầu tụ đạt giá trị cực đại thì uRL vuông pha với u.
Ta có giản đồ véc tơ như hình bên
Khi đó u R L 2 U 0 R L 2 + u 2 U 0 2 = 1 ⇔ 50 2 . 6 U 0 R L 2 + 150 2 . 6 U 0 2 = 1 (1)
Mặt khác, từ hệ thức lượng trong tam giác vuông ta có:
1
U
0
R
L
2
+
1
U
0
2
=
1
U
0
R
2
=
1
150
2
.
2
(2)
Giải (1) và (2) ta thu được U 0 2 = 180000 ⇒ U 0 = 300 2 ⇒ U = 300 (V)

Giải thích: Đáp án B
Ta có: 
Tổng trở của mạch khi đó: 
Khi URmax ta có: 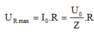
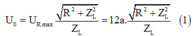
Góc lệch pha giữa u và i trong mạch: 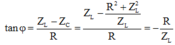
Góc lệch pha giữa uRL và i trong mạch:  và u vuông pha nhau
và u vuông pha nhau
Khi đó: 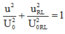
Xét tỉ số: 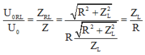

![]()
Khi u = 16a thì uC = 7a ![]()
Thay (1) và (2) vào (3):
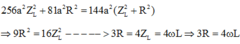

Đáp án B
Phương pháp giải: Sử dụng các công thức của bài toán điện dung của tụ điện thay đổi.
Điều chỉnh C để điện áp hiệu dụng hai đầu tụ đạt giá trị cực đại thì uRL vuông pha với u.
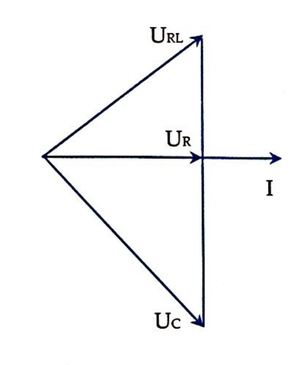


Đáp án C
+ Điện trở của mạch R = u R i = 20 Ω
Điện áp trên điện trở và trên tụ điện luôn vuông nhau tại cùng một thời điểm bất kì, ta có:

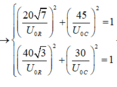
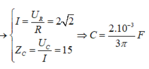


Ta có R = 3 Z L . Nối tắt tụ và khi không nối tắt tụ thì điện áp hiệu dụng trên điện trở R cũng không đổi → Z C = 2 Z L
→ U 0 R = U 0 R R 2 + Z L − Z C 2 = 200 3 Z L 3 Z L 2 + Z L − 2 Z L 2 = 100 3 V
→ tan φ = Z L − Z C R = Z L − 2 Z L 3 Z L = − 1 3 → u chậm pha hơn i một góc 30 độ
Biểu diễn vecto quay cho điện áp u và dòng điện i tại thời điểm t. Dòng điện i tại thời điểm t + π 6 ω = t + T 12 ứng với góc quét 30 độ .
→ u R = U 0 R cos 60 0 = 50 3 V.
Đáp án C
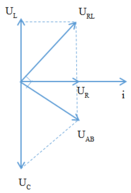
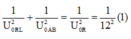
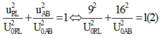
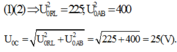
U U U i RL R m
C thay đổi để UC max thì uRL vuông pha với u mạch.
Từ giản đồ véc tơ ta có: \(\frac{1}{U_R^2}=\frac{1}{U_{RL}^2}+\frac{1}{U_m^2}=\frac{1}{75^2}\left(1\right)\)
Do sự vuông pha nên: \(\left(\frac{u_{RL}}{U_{0RL}}\right)^2+\left(\frac{u_m}{U_{0m}}\right)^2=1\Rightarrow\left(\frac{25\sqrt{6}}{U_{0RL}}\right)^2+\left(\frac{75\sqrt{6}}{U_{0m}}\right)^2=1\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình, giải ra ta được: \(U_{0m}=300V\)
\(\Rightarrow U_m=150\sqrt{2}V\)
Đáp án D.