

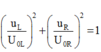
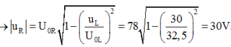
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



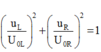
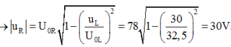

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

Đáp án A
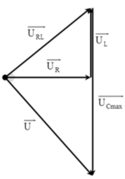
Phương pháp: Áp dụng giản đồ vectơ trong mạch điện xoay chiều
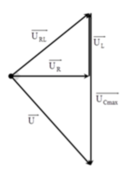
Cách giải: Biểu diễn vecto các điện áp.
Khi UCmax thì điện áp hai đầu mạch vuông pha với điện áp hai đầu đoạn mạch RL
+ Áp dụng hệ thức lượng trong tam giác, ta có: U 2 0 R = U 0 L ( U 0 C m a x - U 0 L )
+ Mặt khác, ta để ý rằng, tại thời điểm t
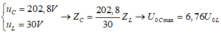
+ Thay vào phương trình hệ thức lượng ta tìm được U 0 L = 32 , 5 V
Với hai đại lượng vuông pha uL và uR ta luôn có
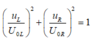
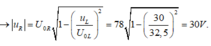

Chọn A.
Ta có uLvà uC luôn ngược pha nhau 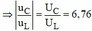
Lại có 
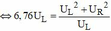
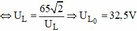
Lại có uR, uL luôn vuông pha
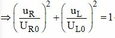
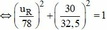
![]()

Bài 1:
Để công suát tiêu thụ trê mạch cực đại thì:
\((R+r)^2=(R_1+r)(R_1+r)\)
\(\Rightarrow (R+10)^2=(15+10)(39+10)\)
\(\Rightarrow R=25\Omega\)
Bài 2: Có hình vẽ không bạn? Vôn kế đo hiệu điện thế của gì vậy?

\(2LC\omega^2=1\rightarrow2Z_L=Z_C\rightarrow2u_L=-uc\)
\(u_m=u_R+u_L+u_c=40+\left(-30\right)+60=70V\)
Chọn B

Khi Uc1=40V thì có Um= \(\sqrt{60^2+\left(120-40\right)^2}\)=100 V và UL=2Ur là không đổi
Khi U2=80V Thì Um=1002= Ur2 +(2Ur-80)2 Giải ra đk Ur= 73,76V

Giải thích: Đáp án C
Cách giải 1:
Ta có: uRL = U0RL = 84,5V
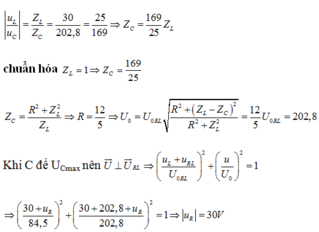
Cách giải 2. (Cách hiện đại. Dành cho học sinh giỏi).
Ta có: 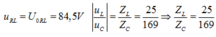
Khi C thay đổi để UCmax thì:
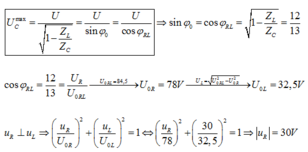
Cách giải 3.
Ta có: U0RL = 84,5V. Khi C thay đổi để UCmax thì ta có
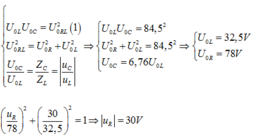
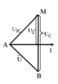
Chú ý: Công thức (1) suy ra từ đi theo hai hướng tư duy như sau:
*Học sinh giỏi: Dùng giản đồ. Khi C thay đổi để UCmax thì ∆AMB vuông tại A.
suy ra ngay ![]() . (không cần nhớ công thức)
. (không cần nhớ công thức)
*Học sinh khá: Nhớ công thức khi C thay đổi để UCmax thì ta có
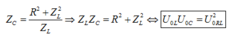

Đáp án C.
lúc đầu ta có :
UMB=2UR => ZMB=2R <=> ZC=\(\sqrt{3}\)R mà C=\(\frac{L}{R^2}\) => ZL=\(\frac{R}{\sqrt{3}}\)
lúc sau ta có Uc' max :
Zc'.ZL=R2+ \(Z^2_L\) => Zc'=\(\frac{4R}{\sqrt{3}}\)
\(\text{tanφ}=\frac{Z_L-Z_C}{R}\Rightarrow\tan\varphi=-\sqrt{3}\Rightarrow\varphi=-\frac{\pi}{3}\)