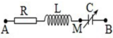
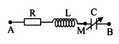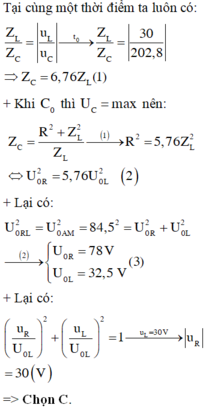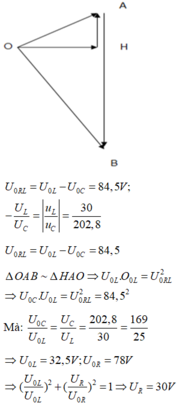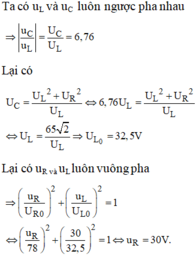Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
Cách giải 1: Ta có: u R L = U 0 R L = 84 , 5 V
u L u C = Z L Z C = 30 202 , 8 = 25 169 ⇒ Z C = 169 25 Z L chuẩn hóa Z L = 1 ⇒ Z C = 169 25
Z C = R 2 + Z L 2 Z L ⇒ R = 12 5 ⇒ U 0 = U 0 R L R 2 + Z L − Z C 2 R 2 + Z L 2 = 12 5 U 0 R L = 202 , 8
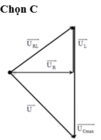
Khi C để U C max nên U → ⊥ U R L → ⇒ u L + u R U 0 R L 2 + u U 0 2 = 1
⇒ 30 + u R 84 , 5 2 + 30 + 202 , 8 + u R 202 , 8 2 = 1 ⇒ u R = 30 V
Cách giải 2. (Cách hiện đại. Dành cho học sinh giỏi).
Ta có: u R L = U 0 R L = 84 , 5 V → u L u C = Z L Z C = 25 169 ⇒ Z L Z C = 25 169
Khi C thay đổi để U C max thì:
U C m a x = U 1 − Z L Z C = U s i n φ 0 = U c o s φ R L ⇒ s i n φ 0 = c o s φ R L = 1 − Z L Z C = 12 13
c o s φ R L = 12 13 = U 0 R U 0 R L → U 0 R L = 84 , 5 U 0 R = 78 V → U L = U 0 R L 2 − U 0 R 2 U 0 L = 32 , 5 V u R ⊥ u L ⇒ u R U 0 R 2 + u L U 0 L 2 = 1 ⇔ u R 78 2 + 30 32 , 5 2 = 1 ⇒ u R = 30 V
Cách giải 3.
Ta có: U 0 R L = 84 , 5 V . Khi C thay đổi để U C max thì ta có:
U 0 L U 0 C = U 0 R L 2 ( 1 ) U 0 R L 2 = U 0 R 2 + U 0 L 2 U 0 C U 0 L = Z C Z L = u C u L ⇒ U 0 L U 0 C = 84 , 5 2 U 0 R 2 + U 0 L 2 = 84 , 5 2 U 0 C = 6 , 76 U 0 L ⇒ U 0 L = 32 , 5 V U 0 R = 78 V
u R 78 2 + 30 32 , 5 2 = 1 ⇒ u R = 30 V
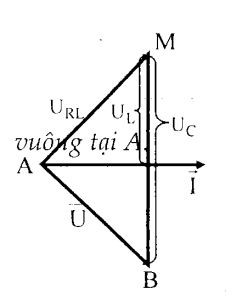
Chú ý: Công thức (1) suy ra từ đi theo hai hướng tư duy như sau:
Học sinh giỏi: Dùng giản đồ. Khi C thay đổi để U C max thì Δ A M B suy ra ngay U 0 L U 0 C = U 0 R L 2 . . (không cần nhớ công thức).
Học sinh khá: Nhớ công thức khi C thay đổi để U C max thì ta có
Z C = R 2 + Z L 2 Z L ⇒ Z L Z C = R 2 + Z L 2 ⇔ U 0 L U 0 C = U 0 R L 2

Chọn đáp án A.
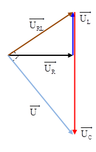
+ Bài toán Z C biến thiên để U C m a x . Khi U C m a x thì điện áp hai đầu mạch vuông pha với điện áp hai đầu đoạn mạch RL
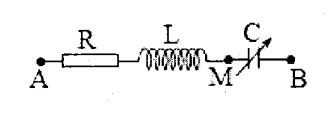
+ Áp dụng hệ thức lượng trong tam giác, ta có:
U 0 R 2 = U 0 L ( U 0 C - U 0 L )
Mặt khác, ta để ý rằng, tại thời điểm t
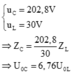
Thay vào phương trình hệ thức lượng ta tìm được U 0 L = 32 , 5 V = 32,5V
Với hai đại lượng vuông pha u L và u R ta luôn có:
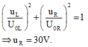

Đáp án A
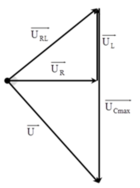
Biểu diễn vecto các điện áp.
Khi U max thì điện áp hai đầu mạch vuông pha với điện áp hai đầu đoạn mạch RL
+ Áp dụng hệ thức lượng trong tam giác, ta có:
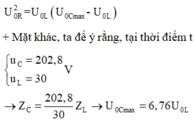
+ Thay vào phương trình hệ thức lượng ta tìm được U 0 L =32,5V
Với hai đại lượng vuông pha u L và u R ta luôn có:
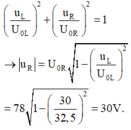

Chọn đáp án C
Cách 1: Giải truyền thống
Khi C thay đổi để U C max ta có:
C c max = U 1 − Z L Z C 0 ⇔ 160 = 80 1 − Z L Z C 0 → S H I F T − S O L V E Z L Z C 0 = 3 4 ⇒ Z C 0 = 4 3 Z L . Z C 0 = R 2 + Z L 2 Z L ⇔ 4 3 Z L = 20 3 2 + Z L 2 Z L ⇒ Z L = 60 Ω ⇒ Z C 0 = 80 Ω i ¯ = u ¯ Z ¯ = 80 2 ∠ − π 4 20 3 + 60 − 80 i = 2 2 ∠ − π 12
Cách 2: Cách hiện đại (có sử dụng yếu tố góc).
U C max = U − sin φ 0 ⇔ 160 = 80 − sin φ 0 ⇒ sin φ 0 = − 1 2 ⇒ φ 0 = − π 6 ⇒ φ 0 = − π 12 I 0 = U 0 R cos φ 0 = 80 2 20 3 . cos arcsin − 1 2 = 2 2 ⇒ i = 2 2 cos 100 π t − π 12 V