Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giá trị của R để công suất tiêu thụ trên biến trở cực đại R 2 = r 2 + Z L − Z C 2 .
Kết hợp với
U = 1 , 5 U R ⇒ R + r 2 + Z L − Z C 2 = 2 , 25 R 2 Z = 1 , 5 R
Để đơn giản, ta chuẩn hóa
Z L − Z C = 1 ⇒ r = 1 63 R = 8 63 Z = 8 63 ⇒ cos φ = R Z = 0 , 75
Đáp án A

Công suất tiêu thụ trên biến trở đạt giá trị cực đại khi R 2 = r 2 + Z L − Z C 2
Chuẩn hóa Z L − Z C 2 = 1 ⇒ R 2 = 1 + r 2
Mặc khác
U R = U R R + r 2 + Z L − Z C 2 ⇔ 1 1 , 5 = 1 + r 2 1 + r 2 + r 2 + 1 ⇒ r = 0 , 125 R = 1 , 008
Hệ số công suất của mạch
cos φ = R + r R + r 2 + Z L − Z C 2 = 0 , 749
Đáp án D

R 1 R 2 = 100 2 U C 1 = 2 U C 2 ⇒ R 1 R 2 = 100 2 I 1 = 2 I 2 ⇒ R 1 R 2 = 100 2 R 2 2 + 100 2 = 4 R 1 2 + 4.100 2
→ Ta có phương trình R 2 2 − 2 R 1 R 2 − 4 R 1 2 = 0
→ R 2 = 4 R 1 .
Thay vào phương trình trên, ta tìm được R 1 = 50 Ω v à R 2 = 200 Ω .
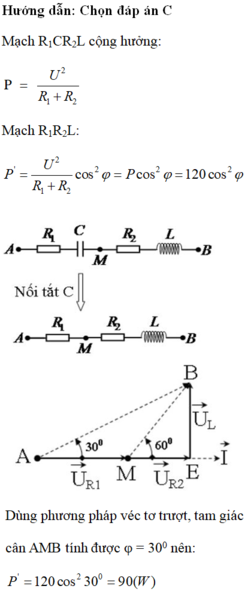
Đáp án C
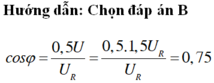

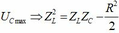

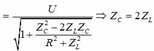
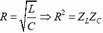
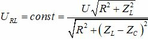
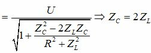

R thay đổi để công suất tiêu thụ trên biến trở lớn nhất khi: \(R=Z_{đoạn-còn-lại}\)
\(\Rightarrow R=\sqrt{r^2+\left(Z_L-Z_C\right)^2}\)
\(U_{AB}=1,5U_R\Leftrightarrow Z=1,5R\)
\(\Rightarrow\left(R+r\right)^2+\left(Z_L-Z_C\right)^2=1,5^2.R^2\)
\(\Rightarrow R^2+2Rr+r^2+\left(Z_L-Z_C\right)^2=1,5^2.R\)
\(\Rightarrow R^2+2Rr+R^2=1,5^2.R\)
\(\Rightarrow r=0,125R\)
Hệ số công suất: \(\cos\varphi=\frac{R+r}{Z}=\frac{1,125R}{Z}=1,125.\frac{1}{1,5}=0,75\)
Chọn D
Em cảm ơn thầy rất nhiều........