Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án A
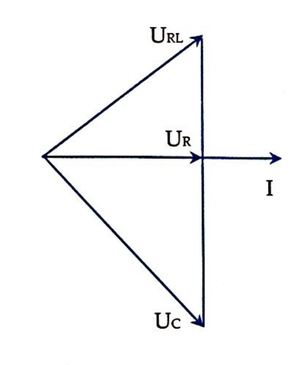
Phương pháp: Sử dụng giản đồ vecto kết hợp kĩ năng đọc đồ thị
CÁCH GIẢI: Từ đồ thị ta suy ra được:
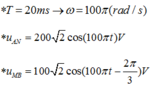
Từ giản đồ ta có:
![]()
![]()
![]()
![]()
![]()

Đáp án A
Phương pháp: Sử dụng giản đồ vecto kết hợp kĩ năng đọc đồ thị
Cách giải: Từ đồ thị ta suy ra được:
T = 20 m s → ω = 100 π ( r a d / s )
u A N = 200 2 cos ( 100 π t ) V
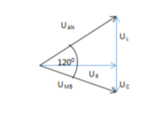
Từ đó có thể vẽ giản đồ:
Từ giản đồ ta có:
U R = U A N cos α = U M B cos ( 120 0 - α )
![]()
U L = U A N sin α ≈ 189 V ; U C = U M B sin ( 120 0 - α ) ≈ 75 , 6 V U = U 2 R + ( U L - U C ) 2 ≈ 131 V → U 0 = U 2 = 185 V

ü Đáp án B
+ Từ đồ thị ta có ![]() , tại
, tại ![]() và có xu hướng tăng
và có xu hướng tăng
→ ![]()
Để đơn giản, ta chọn ![]()
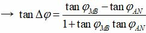
![]()

Từ đồ thị, ta thấy rằng ω R = 2 ω C → n = 4.
Áp dụng công thức chuẩn hóa .
U L m a x = U 1 − n − 2 ⇒ U L m a x U = 1 1 − n − 2 = 1 , 03
Đáp án C

Đáp án: B
Sử dụng các công thức của bài toán điện dung của tụ điện thay đổi.
Điều chỉnh C để điện áp hiệu dụng hai đầu tụ đạt giá trị cực đại thì uRL vuông pha với u.
Ta có giản đồ véc tơ như hình bên
Khi đó u R L 2 U 0 R L 2 + u 2 U 0 2 = 1 ⇔ 50 2 . 6 U 0 R L 2 + 150 2 . 6 U 0 2 = 1 (1)
Mặt khác, từ hệ thức lượng trong tam giác vuông ta có:
1
U
0
R
L
2
+
1
U
0
2
=
1
U
0
R
2
=
1
150
2
.
2
(2)
Giải (1) và (2) ta thu được U 0 2 = 180000 ⇒ U 0 = 300 2 ⇒ U = 300 (V)

Đáp án B
Phương pháp giải: Sử dụng các công thức của bài toán điện dung của tụ điện thay đổi.
Điều chỉnh C để điện áp hiệu dụng hai đầu tụ đạt giá trị cực đại thì uRL vuông pha với u.