Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có \(\left(log^b_a+log^a_b+2\right)\left(log^b_a-log_{ab}^b\right).log_b^a-1=\left(log^b_a+log^a_b+2\right)\left(log^b_a.log_b^a-log_{ab}^b.log_b^a\right)-1=\left(log^b_a+log^a_b+2\right)\left(1-\frac{1}{log_b^{ba}}log_b^a\right)-1=\left(log^b_a+log^a_b+2\right)\left(1-\frac{1}{1+log^a_b}log^a_b\right)-1=\left(log^b_a+log^a_b+2\right)\frac{1}{1+log^a_b}-1=\left(log^a_b+\frac{1}{log^a_b}+2\right)\frac{1}{1+log^a_b}-1=\frac{\left(1+log^a_b\right)^2}{log^a_b}\frac{1}{1+log^a}-1=\frac{1+log^a_b}{log_b^a}-1=\frac{1}{log_b^a}\)
ta có:
\(\left(log^b_a+\frac{1}{log^b_a}+2\right)\left(log^b_a-\frac{1}{log^{ab}_a}\right)log^a_b-1\)\(=\frac{\left(log^b_a+1\right)^2}{log^b_a}\left(log^b_a-\frac{1}{1+log^b_a}\right)log^a_b-1\)\(=\frac{\left(log^b_a+1\right)^2}{log^b_a}\left(1-\frac{log^a_b}{1+log^b_a}\right)-1\)\(==\frac{\left(log^b_a+1\right)^2}{log^b_a}\left(\frac{1}{1+log^b_a}\right)-1=\frac{1+log^b_a}{log^b_a}-1=\frac{1}{log^b_a}\)
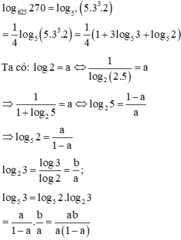

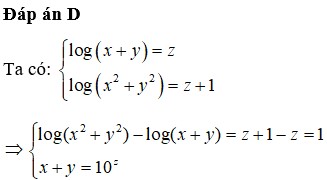

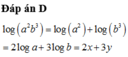
Đáp án B
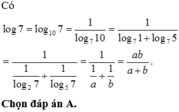
Ta có log 15 10 = log 5 10 log 5 15 = log 5 2 . 5 log 5 3 . 5 = log 5 2 + 1 log 5 3 + 1 mà log 5 3 = 1 a ; log 5 2 = log 5 4 2 = 1 2 b .
Khi đó log 15 10 = 1 2 b + 1 1 a + 1 = 2 b + 1 2 b a + 1 a = a 2 b + 1 2 b a + 1 = a + 2 a b 2 b + 2 a b .