Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi AD, BE, CF là ba đường cao của tam giác ABC cắt nhau tại H
1. Theo định lý Pythagoras, ta có: \(AB^2+HC^2=\left(AD^2+DB^2\right)+\left(HD^2+DC^2\right)=\left(AD^2+DC^2\right)+\left(DB^2+HD^2\right)=AC^2+HB^2\)(1)
\(BC^2+HA^2=\left(BE^2+EC^2\right)+\left(AE^2+HE^2\right)=\left(BE^2+AE^2\right)+\left(EC^2+HE^2\right)=AB^2+HC^2\)(2)
Từ (1) và (2) suy ra \(AB^2+HC^2=AC^2+HB^2=BC^2+HA^2\)(đpcm)
2. Ta có: \(BC.HA=BC.AD-BC.HD=2S-2S_{BHC}\)
Tương tự: \(AB.HC=2S-2S_{AHB}\); \(CA.HB=2S-2S_{AHC}\)
Suy ra \(AB.HC+BC.HA+CA.HB=6S-2S=4S\)(đpcm)

a) Áp dụng định lí pitago.
Ta có: \(AB^2=AD^2+BD^2=BE^2+AE^2\)
\(HC^2=HD^2+DC^2=HE^2+EC^2\)
=> \(AB^2+HC^2=AD^2+BD^2+HD^2+DC^2\)
\(=\left(AD^2+DC^2\right)+\left(BD^2+HD^2\right)=AC^2+BH^2\) (1)
và \(AB^2+HC^2=BE^2+AE^2+HE^2+EC^2\)
\(=\left(BE^2+EC^2\right)+\left(AE^2+HE^2\right)=BC^2+AH^2\)(2)
Từ (1) , (2) Ta có: \(AB^2+HC^2=AC^2+HB^2=BC^2+HA^2\)
b) Ta có: \(S_{AHB}+S_{AHC}+S_{BHC}=S_{ABC}=S\)
\(AB.HC=AB\left(CF-FH\right)=AB.CF-AB.FH\)
\(=2S_{ABC}-2S_{AHB}=2S-2S_{ABH}\)
Tương tự: \(BC.HA=2S-2S_{BHC}\)
\(CA.HB=2S-2S_{AHC}\)
Cộng lại ta có:
\(AB.HC+BC.AH+CA.HB=6S-2\left(S_{AHB}+S_{AHC}+S_{BHC}\right)\)
\(=6S-2S=4S\)(đpcm)


\(OE=OB=\dfrac{1}{2}BC\Rightarrow\widehat{OBE}=\widehat{OEB}\)
\(\widehat{AHE}=\widehat{BHO}\) ; \(\widehat{BHO}+\widehat{HBD}=90^0\)
\(\Rightarrow\widehat{AHE}+\widehat{HBD}\left(\widehat{OBE}\right)=90^0\)
\(\Rightarrow\widehat{AHE}+\widehat{OEB}=90^0\)
\(IE=IH=r\Rightarrow\widehat{AHE}=\widehat{IEH}\)
\(\Rightarrow\widehat{IEH}+\widehat{OEB}=90^0\Rightarrow IE\perp OE\)

Lời giải:
a. Ta có:
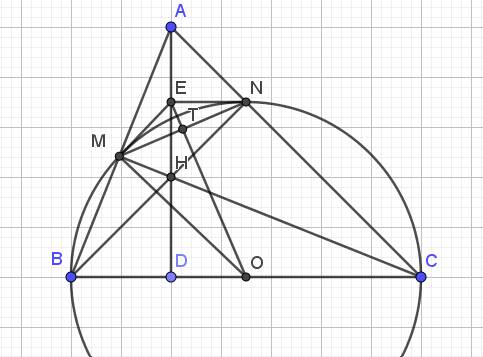
$\widehat{BNC}=\widehat{BMC}=90^0$ (góc nt chắn nửa đường tròn - cung BC)
$\Rightarrow BN\perp AC, CM\perp AB$
Tam giác $ABC$ có 2 đường cao $BN, CM$ cắt nhau tại $H$ nên $H$ là trực tâm của tam giác $ABC$.
b. Gọi $D$ là giao của $AH$ và $BC$. Do $H$ là trực tâm tam giác $ABC$ nên $AH\perp BC$ tại $D$.
Tam giác $BMC$ vuông tại $M$
$\Rightarrow$ trung tuyến $MO= \frac{BC}{2}=BO$ (đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền)
$\Rightarrow BOM$ là tam giác cân tại $O$
$\Rightarrow \widehat{OMB}=\widehat{OBM}=90^0-\widehat{BCM}$
$=90^0-\widehat{DCH}=\widehat{MHA}=\widehat{MHE}(1)$
$CM\perp AB$ nên $AMH$ là tam giác vuông tại $M$
$\Rightarrow ME=\frac{AH}{2}=EH$ (đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền)
$\Rightarrow MEH$ cân tại $E$
$\Rightarrow \widehat{MHE}=\widehat{EMH}(2)$
Từ $(1); (2)\Rightarrow \widehat{OMB}=\widehat{EMH}$
$\Rightarrow \widehat{OMB}+\widehat{OMC}=\widehat{EMH}+\widehat{OMC}$
$\Rightarrow \widehat{BMC}=\widehat{EMO}$
$\Rightarrow \widehat{EMO}=90^0$
$\Rightarrow EM\perp MO$ nên $EM$ là tiếp tuyến $(O)$
c.
Ta có:
$EM=\frac{AH}{2}=EN$
$OM=ON$
$\Rightarrow EO$ là trung trực của $MN$
Gọi $T$ là giao điểm $EO, MN$ thì $EO\perp MN$ tại $T$ và $T$ là trung điểm $MN$.
Xét tam giác $EMO$ vuông tại $M$ có $MT\perp EO$ thì:
$ME.MO = MT.EO = \frac{MN}{2}.EO$
$\Rightarrow 2ME.MO = MN.EO$

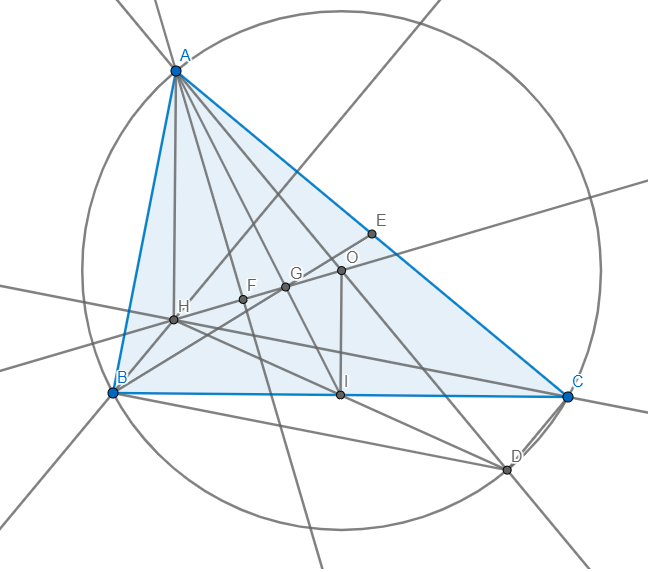
a) chắc đề hỏi là tứ giác BHCD là hình gì chứ ko có điểm K
Vì AD là đường kính \(\Rightarrow\left\{{}\begin{matrix}\angle ACD=90\\\angle ABD=90\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}CD\bot AC\\BD\bot AB\end{matrix}\right.\)
mà \(\left\{{}\begin{matrix}BH\bot AC\\CH\bot AB\end{matrix}\right.\Rightarrow\) \(CD\parallel BH,BD\parallel CH\) \(\Rightarrow BHCD\) là hình bình hành
b) Vì BHCD là hình bình hành có I là trung điểm BC
\(\Rightarrow H,I,D\) thẳng hàng và I cũng là trung điểm HD
Xét \(\Delta AHD\) có O là trung điểm AD,I là trung điểm HD
\(\Rightarrow OI\) là đường trung bình \(\Rightarrow OI=\dfrac{1}{2}AH\Rightarrow AH=2OI\)
c) AI cắt HO tại G'.
Vì \(OI\parallel AH\) \(\Rightarrow\dfrac{AH}{OI}=\dfrac{AG'}{G'I}\Rightarrow\dfrac{AG'}{G'I}=2\Rightarrow\dfrac{AG'}{AI}=\dfrac{2}{3}\)
\(\Rightarrow G'\) là trọng tâm tam giác ABC \(\Rightarrow G\equiv G'\Rightarrow\) đpcm
Vì \(OI\parallel AH\) \(\Rightarrow\dfrac{GH}{GO}=\dfrac{AH}{OI}=2\Rightarrow GH=2GO\)
d) Kẻ \(AF\bot HO\) \(\Rightarrow\left\{{}\begin{matrix}S_{AOG}=\dfrac{1}{2}.AF.OG\\S_{AHG}=\dfrac{1}{2}.AF.HG\end{matrix}\right.\)
mà \(GH=2GO\Rightarrow S_{AHG}=2S_{AOG}\)