Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(C) giao Ox tại 3 điểm <=> x^3-(2m+1)x^2-9x=0 có 3nghiệm pbiệt
<=> x( x^2- ( 2m+1)x-9)=0 có 3 nghiệm pbiệt
<=> x=0
x^2- ( 2m+1)x-9=0 (*)có 2 nghiệm pbiệt <=> denta >0
gọi x1, x2 là 2 nghiệm của (*)
3 nghiệm của đề là x1;0 ; x2
ta có x1+x2=0 dùng viet
phuong trinh hoanh do giao diem la: x3-(2m+1)x2-9x=0. <=> x[x2 -(2m+1)x-9] =0 ta giai dc x=o va x2-(2m+1)x-9=0 ta dat g(x)=x2-(2m+1)x-9 de cm cat truc hoanh tai 3 diem pb thi g(x)=o phai co 2 nghiem pb khac 0. <=>Δ>0 =>m goi x1, x2 la nghiem cua g(x) de lap thanh cap so cong thi x2=9x1 Ap dung vi-et tim ra la dc![]()

a) y′ = 3 x 2 + 2(m + 3)x + m
y′ = 0 ⇔ 3 x 2 + 2(m + 3)x + m = 0
Hàm số đạt cực trị tại x = 1 thì:
y′(1) = 3 + 2(m + 3) + m = 3m + 9 = 0 ⇔ m = −3
Khi đó,
y′ = 3 x 2 – 3;
y′′ = 6x;
y′′(1) = 6 > 0;
Suy ra hàm số đạt cực tiểu tại x = 1 khi m = 3.
b) y′ = −( m 2 + 6m) x 2 − 4mx + 3
y′(−1) = − m 2 − 6m + 4m + 3 = (− m 2 − 2m – 1) + 4 = −(m + 1)2 + 4
Hàm số đạt cực trị tại x = -1 thì :
y′(−1) = − ( m + 1 ) 2 + 4 = 0 ⇔ ( m + 1 ) 2 = 4
⇔ 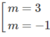
Với m = -3 ta có y’ = 9 x 2 + 12x + 3
⇒ y′′ = 18x + 12
⇒ y′′(−1) = −18 + 12 = −6 < 0
Suy ra hàm số đạt cực đại tại x = -1.
Với m = 1 ta có:
y′ = −7 x 2 − 4x + 3
⇒ y′′ = −14x − 4
⇒ y′′(−1) = 10 > 0
Suy ra hàm số đạt cực tiểu tại x = -1
Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.

Nhìn câu vẽ đồ thị kia là tiêu rồi bạn
Bạn tự vẽ đồ thị, mấy câu sau mình làm thì được

+ Phương trình hoành độ giao điểm của đồ thị C và trục Ox:
x3- 3( m+ 1) x2+ 2( m 2+ 4m+1 )= 0
hay ( x- 2) ( x2-( 3m+ 1) x+ 2m2+ 2m) =0
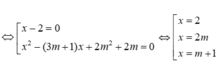
Yêu cầu bài toán
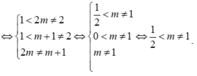
Vậy ½< m và m≠ 1.
Chọn A.

Phương trình hoành độ giao điểm của đồ thị với trục hoành là :
\(x^3-2x^2+\left(1-m\right)x+m=0\left(1\right)\)
Biến đổi tương đương phương trình này :
\(\left(1\right)\Leftrightarrow x^3-2x^2+x-mx+m=0\)
\(\Leftrightarrow x\left(x^2-2x+1\right)-m\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-x-m\right)=0\Leftrightarrow x=1\) hoặc \(x^2-x-m=0\left(2\right)\)
Gọi \(x_1,x_2\) là nghiệm của phương trình (2) thì :
\(t^2+x_1^2+x_2^2< 4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2< 3\Leftrightarrow m< 1\) (*)
Yêu cầu bài toán tương đương với (2) có hai nghiệm phân biệt \(x_1;x_2\ne1\) thỏa mãn điều kiện (*)
\(\Leftrightarrow\begin{cases}\Delta=1+4m>0\\1^2-1-m\ne0\\m< 1\end{cases}\)\(\Leftrightarrow\begin{cases}-\frac{1}{4}< m< 1\\m\ne0\end{cases}\)
b) Xét pt hoành độ giao điểm của hàm số đã cho và Ox là \(2x^3+2\left(6m-1\right)x^2-3\left(2m-1\right)x-3\left(1+2m\right)=0\) (*)
Ta thấy \(x=1\) là nghiệm của pt trên. Lập sơ đồ Horner:
Do đó pt (*)
\(\Leftrightarrow\left(x-1\right)\left(2x^2+12mx+6m+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\2x^2+12mx+6m+3=0\end{matrix}\right.\)
Xét pt \(2x^2+12mx+6m+3=0\) (1)
Ycbt \(\Leftrightarrow\) pt (1) có 2 nghiệm phân biệt \(x_1,x_2\) khác 1 và thỏa mãn \(x_1^2+x_2^2=27\)
Có \(\Delta'=\left(6m\right)^2-2\left(6m+3\right)=36m^2-12m-6>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>\dfrac{1+\sqrt{7}}{6}\\m< \dfrac{1-\sqrt{7}}{6}\end{matrix}\right.\)
Có 2 nghiệm khác 1 \(\Leftrightarrow2.1^2+12m.1+6m+3\ne0\)
\(\Leftrightarrow18m+5\ne0\)
\(\Leftrightarrow m\ne-\dfrac{5}{18}\)
Theo định lý Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=-6m\\x_1x_2=\dfrac{6m+3}{2}\end{matrix}\right.\)
Để \(x_1^2+x_2^2=27\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=27\)
\(\Leftrightarrow\left(-6m\right)^2-2.\dfrac{6m+3}{2}=27\)
\(\Leftrightarrow36m^2-6m-3=27\)
\(\Leftrightarrow6m^2-m-5=0\)
\(\Leftrightarrow6m^2-6m+5m-5=0\)
\(\Leftrightarrow6m\left(m-1\right)+5\left(m-1\right)=0\)
\(\Leftrightarrow\left(m-1\right)\left(6m+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\left(nhận\right)\\m=-\dfrac{5}{6}\left(nhận\right)\end{matrix}\right.\)
Vậy \(m=1\) hoặc \(m=-\dfrac{5}{6}\) thỏa ycbt.
c) Xét pt \(x^3-3mx^2+\left(3m-1\right)x+6m=0\) (*)
Ta thấy (*) có nghiệm \(x=-1\). Lập sơ đồ Horner:
Vậy (*) \(\Leftrightarrow\left(x+1\right)\left(x^2-\left(3m+1\right)x+6m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2-\left(3m+1\right)x+6m=0\end{matrix}\right.\)
Tới đây thì làm tương tự câu b) nhé.