K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
0
1D
0
26 tháng 2 2022
a: \(f\left(x\right)+g\left(x\right)=x^3-3x^2+6x-8+x^3-6x^2+12x-8\)
\(=2x^3-9x^2+18x-16\)
b: \(f\left(1\right)=1^3-3\cdot1^2+6\cdot1-8=1-3+6-8=-2+6-8=4-8=-4\)
\(g\left(-1\right)=-6\cdot\left(-1\right)^2+\left(-1\right)^3-8+12\cdot\left(-1\right)\)
\(=-6\cdot1-1-8-12\)
=-6-21
=-27
c: f(x)-g(x)=0
=>f(x)=g(x)
\(\Leftrightarrow x^3-3x^2+6x-8=x^3-6x^2+12x-8\)
\(\Leftrightarrow3x^2-6x=0\)
=>3x(x-2)=0
=>x=0 hoặc x=2
26 tháng 2 2022
Bài 7:
Đặt f(x)=a; g(x)=b
Theo đề, ta có: \(\left\{{}\begin{matrix}a+b=5x^2-2x+3\\a-b=x^2-2x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=6x^2-4x+8\\a-b=x^2-2x+5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=3x^2-2x+4\\g\left(x\right)=3x^2-2x+4-x^2+2x-5=2x^2-1\end{matrix}\right.\)
5 tháng 3 2022
a: \(=\left(2a^2-3a^2-4a^2\right)+\left(-0.5a-2.5a+3a\right)+\left(5-4+7\right)=-5a^2+8\)
b: \(=\left(a^3-a^3\right)+\left(-2a^2-3a^2+4a^2\right)+\left(a+a-a\right)+\left(-5+4\right)=-a^2+a-1\)
c: \(=-b^4+3b^2-3b-1-b^3+1-3b^2+b^4-5+4b^3+5\)
\(=3b^3-3b\)
31 tháng 8 2021
1: Xét ΔABC có AB=AC
nên ΔABC cân tại A
Suy ra: \(\widehat{ABC}=\widehat{ACB}\)
Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
Do đó: ΔABH=ΔACH
Suy ra: \(\widehat{AHB}=\widehat{AHC}\)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
Do đó: AH\(\perp\)BC
8 tháng 10 2020
\(\hept{\begin{cases}2x=5y\\3x+4y=46\end{cases}}\Leftrightarrow\hept{\begin{cases}\frac{x}{\frac{1}{2}}=\frac{y}{\frac{1}{5}}\\3x+4y=46\end{cases}}\Leftrightarrow\hept{\begin{cases}\frac{3x}{\frac{3}{2}}=\frac{4y}{\frac{4}{5}}\\3x+4y=46\end{cases}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{3x}{\frac{3}{2}}=\frac{4y}{\frac{4}{5}}=\frac{3x+4y}{\frac{3}{2}+\frac{4}{5}}=\frac{46}{\frac{23}{10}}=20\)
\(\frac{3x}{\frac{3}{2}}=20\Rightarrow3x=30\Rightarrow x=10\)
\(\frac{4y}{\frac{4}{5}}=20\Rightarrow4y=16\Rightarrow y=4\)
8 tháng 10 2020
2.x=5.y = \(\frac{X}{5}\)=\(\frac{Y}{2}\)=\(\frac{3x+4Y}{3.5+4.2}\)=\(\frac{46}{23}\)=2
\(\frac{X}{5}\)=2 => x=2.5=10
\(\frac{Y}{2}\)=2 =>y=2.2=4
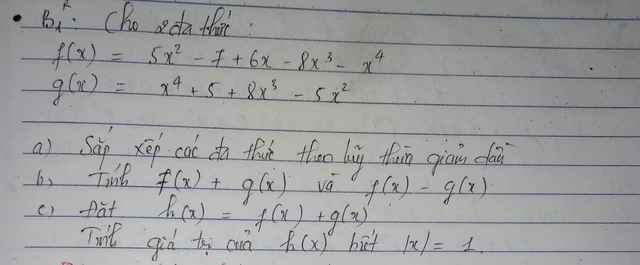
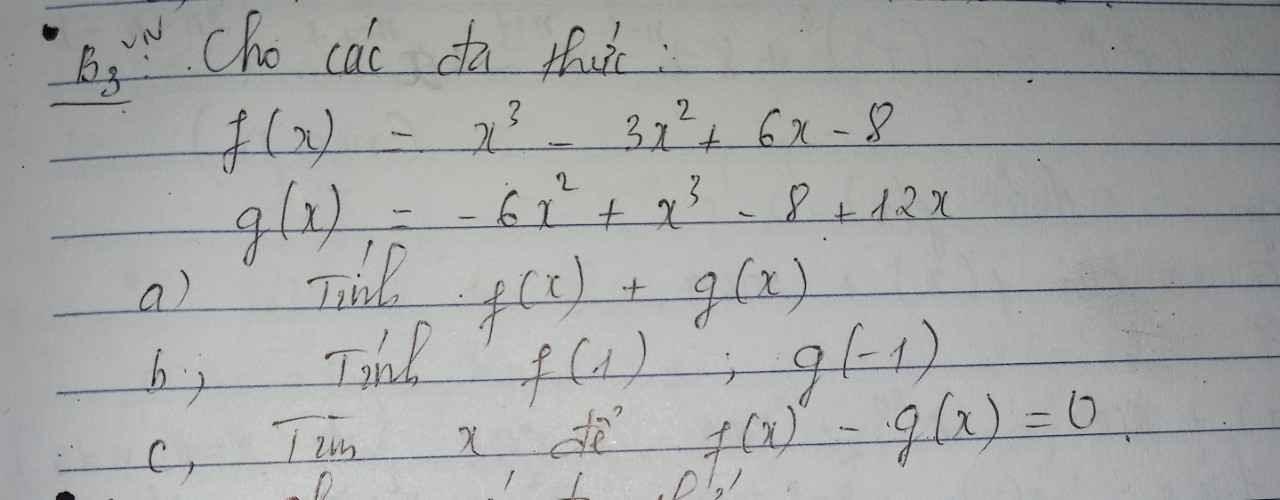
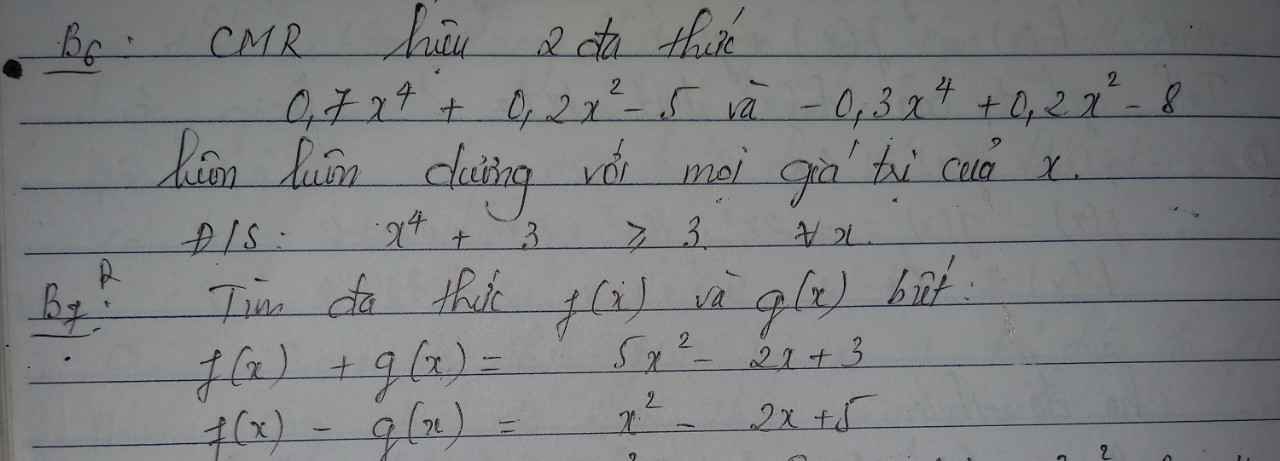
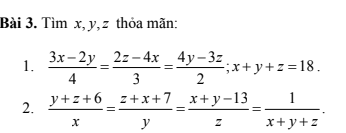
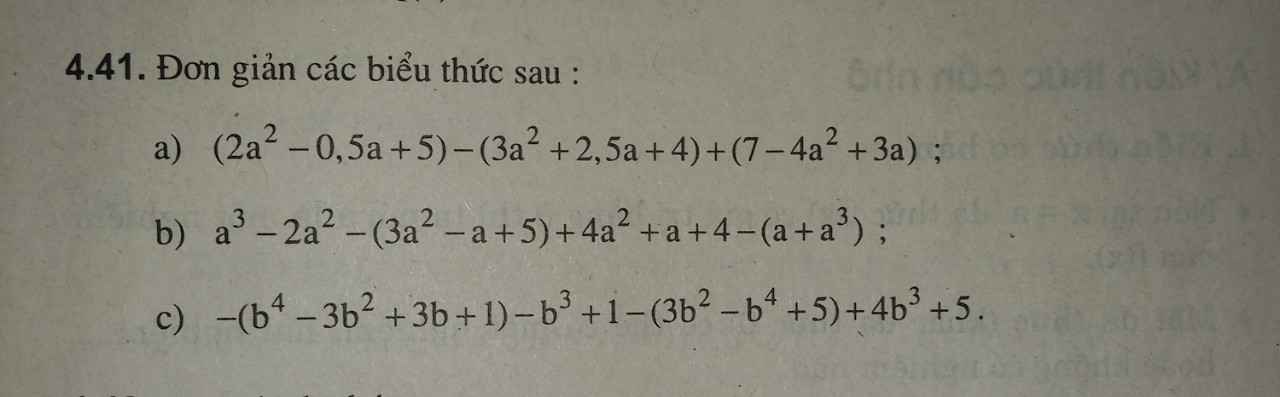
a: \(f\left(x\right)=-x^4-8x^3+5x^2+6x-7\)
\(g\left(x\right)=x^4+8x^3-5x^2+5\)
b: \(f\left(x\right)+g\left(x\right)=6x-2\)
\(f\left(x\right)-g\left(x\right)=-2x^2-16x^3+10x^2+6x-12\)
c: |x|=1 thì x=-1 hoặc x=1
h(-1)=6x(-1)-2=-8
h(1)=6x1-2=4
a/ với f(x)
có : \(-x^4-8x^3+5x^2+6x-7\)
với g(x)
có :\(x^4+8x^3-5x^2+5\)
b, f(x) \(-x^4-8x^3+5x^2+6x-7\)
g(x) \(x^4+8x^3-5x^2\) + 5
f(x)+g(x) = 6x-2