
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1
a) \(2^{11}.64=2^{11}.2^6=2^{17}\)
Do \(16< 17\Rightarrow2^{16}< 2^{17}\)
Vậy \(2^{16}< 2^{11}.64\)
b) Do \(18>17\Rightarrow9^{18}>9^{17}\) (1)
\(9^{18}=\left(3^2\right)^{18}=3^{36}\)
Do \(36< 37\Rightarrow3^{36}< 3^{37}\)
\(\Rightarrow9^{18}< 3^{37}\) (2)
Từ (1) và (2) \(\Rightarrow9^{17}< 3^{37}\)
c) \(2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{222}=\left(3^2\right)^{111}=9^{111}\)
Do \(8< 9\Rightarrow8^{111}< 9^{111}\)
Vậy \(2^{333}< 3^{222}\)
d) \(3^{50}=\left(3^2\right)^{25}=9^{25}\)
Do \(9< 11\Rightarrow9^{25}< 11^{25}\)
Vậy \(3^{50}< 11^{25}\)
e) \(37< 38\Rightarrow3^{37}< 3^{38}\) (1)
Lại có: \(3^{38}=3^{2.19}=\left(3^2\right)^{19}=9^{19}\)
Do \(9< 10\Rightarrow9^{19}< 10^{19}\)
\(\Rightarrow3^{38}< 10^{19}\) (2)
Từ (1) và (2) \(\Rightarrow3^{37}< 10^{19}\)
f) Do \(17>16\Rightarrow17^{14}>16^{14}\) (1)
Do \(32>31\Rightarrow32^{11}>31^{11}\) (2)
Lại có:
\(16^{14}=\left(2^4\right)^{14}=2^{56}\)
\(32^{11}=\left(2^5\right)^{11}=2^{55}\)
Do \(56>55\Rightarrow2^{56}>2^{55}\)
\(\Rightarrow16^{14}>32^{11}\) (3)
Từ (1), (2) và (3) \(\Rightarrow17^{14}>31^{11}\)
Bài 2:
a) \(2^n-64=0\)
\(2^n=64\)
\(2^n=2^6\)
\(n=6\)
b) \(5.3^{n-3}-405=0\)
\(5.3^{n-3}=405\)
\(3^{n-3}=405:5\)
\(3^{n-3}=81\)
\(n-3=4\)
\(n=4+3\)
\(n=7\)
c) \(4^n.8=2^{15}\)
\(\left(2^2\right)^n.2^3=2^{15}\)
\(2^{2n}.2^3=2^{15}\)
\(2^{2n+3}=2^{15}\)
\(2n+3=15\)
\(2n=15-3\)
\(2n=12\)
\(n=12:2\)
\(n=6\)
d) \(3.2^{n+1}+2^{n+2}=160\)
\(2^{n+1}.\left(3+2\right)=160\)
\(2^{n+1}.5=160\)
\(2^{n+1}=160:5\)
\(2^{n+1}=32\)
\(2^{n+1}=2^5\)
\(n+1=5\)
\(n=5-1\)
\(n=4\)

3:
a: 5^n luôn có chữ số tận cùng là 5 với mọi n là số tự nhiên
=>5^100 có chữ số tận cùng là 5
b: \(2^{4k}\) có chữ số tận cùng là 6 với mọi k là số tự nhiên
mà 100=4*25
nên 2^100 có chữ số tận cùng là 6
c: 2023 chia 2 dư 1
mà \(9^{2k+1}\) luôn có chữ số tận cùng là 9
nên \(9^{2023}\) có chữ số tận cùng là 9
d: 2023 chia 4 dư 3
\(7^{4k+3}\left(k\in N\right)\) luôn có chữ số tận cùng là 3
Do đó: \(7^{2023}\) có chữ số tận cùng là 3
Quy luật:
+) các số có c/s tận cg là 0,1,5,6 nâng lên lũy thừa bậc nào (≠0) thì c/s tận cg vẫn là nó.
+) các số có tận cg là 2,4,8 nâng lên lt bậc 4n(n≠0) thì đều có c.s tận cg là 6.
+)các số có c/s tận cg là 3,7,9 nâng lên lt bậc 4n(n≠0) thì đều có c/s tận cg là 1.
+) số có tận cg là 3 khi nâng lên lũy thừa bậc 4n+3 sẽ có tận cùng là 7
+) số có tận cg là 7 khi nâng lên lũy thừa bậc 4n+3 sẽ có tận cùng là 3
+) số có tận cg là 2 khi nâng lên lũy thừa bậc 4n+3 sẽ có tận cùng là 8
+) số có tận cg là 8 khi nâng lên lũy thừa bậc 4n+3 sẽ có tận cùng là 2
+) số có c/s tận cg là 0,1,4,5,6,9 khi nâng lên lũy thừa bậc 4n+3 thì c/s tận cg là chính nó
Bài 3: áp dụng quy luật bên trên
\(a.5^{100}=\overline{..5}\)
\(b.2^{100}=2^{4.25}=\overline{..6}\)
\(c.9^{2023}=\overline{..9}\)
\(d.7^{2023}=7^{4.505+3}=\overline{...3}\)
Bài 4:
\(A=17^{2008}-11^{2008}-3^{2008}\)
\(=\left(\overline{...7}\right)^{4.502}-\left(\overline{..1}\right)^{2008}-\left(\overline{..3}\right)^{4.502}\)
\(=\overline{..1}-\overline{...1}-\overline{...1}\)
\(=\overline{..9}\)
Bài 5:
\(M=17^{25}+24^4-13^{21}\)
\(=\left(\overline{..7}\right)^{4.6}.\left(\overline{..7}\right)+\left(\overline{..4}\right)^{4.1}-\left(\overline{..3}\right)^{4.5}.\left(\overline{..3}\right)\)
\(\overline{..1}.\overline{..7}+\overline{..6}-\overline{..1}.\overline{..3}\)
\(=\overline{...7}+\overline{..6}-\overline{..3}\)
\(=\overline{...0}\)
\(=>M⋮10\)

Cách tìm bội
Ta có thể tìm các bội của một số khác 0 bằng cách nhân số đớ với lần lượt 0, 1, 2, 3, ...
Ví dụ : B(6) = {0 ; 6 ; 12 ; 18 ; ... }
Cách tìm ước.
Ta có thể tìm ước của a (a > 1) bằng cách lần lượt chia a cho các số tự nhiên từ 1 đến a để xem xét a chia hết cho những số nào, khi đó các số ấy là ước của a.
Ví dụ : Ư(16) = {16 ; 8 ; 4 ; 2 ; 1}
Cách tìm ước chung lớn nhất - ƯCLN
Muốn tìm UCLN của của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau:
Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung.
Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là UCLN phải tìm.
Các tìm bội chung nhỏ nhất. (BCNN)
Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta thực hiện theo ba bước sau:
Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung và riêng.
Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.
học tốt
- Bội – ước: Nếu có số tự nhiên a chia hết cho số tự nhiên b ta nói a là bội của b, còn b là ước của a.
* Ước chung (ƯC): Ước chung của hai hay nhiều số là ước của tất cả các số đó.
* Bội chung (BC): Bội chung của hai hay nhiều số là ước của tất cả các số đó.
* ƯCLN của 2 hay nhiều số là số lớn nhất trong tập hợp các ƯC của các số đó.
* Hai hay nhiều số có ƯCLN bằng 1 gọi là các số nguyên tố cùng nhau.
chúc bạn học tốt !



a ƯC ( 16;24) = 1;2;4;8
b ƯC(60;90) = 1;2;3;5;6;10;15;30
c ƯC(24;84)=1;2;3;4;6;12
d ƯC ( 16;60)=1;2;4
h ƯC(18;30;42) =1;2;3;6
e ƯC ( 18;77) = 1
g ƯC (18;90) = 1;2;3;6
k ƯC (26;39;48 ) = 1
Nhớ k cho mình nhe
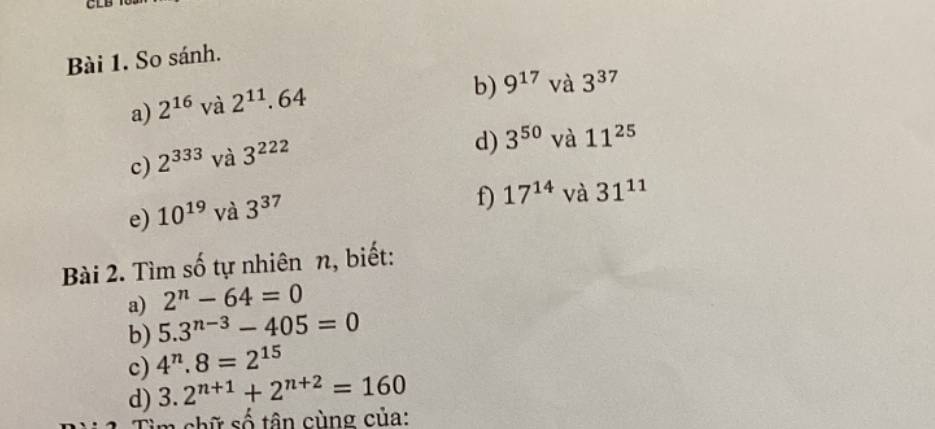

-14,14
ƯC(-14,28) = {1;-1;2;-2;7;-7;14;-14}