Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐÁP ÁN B
CxHy có điều kiện tồn tại là y ≤ 2x + 2
Áp dụng với (CnH2n + 1)m => 2n.m + 1.m ≤ 2n.m + 2
=> m ≤ 2
+) Nếu m = 1 => CnH2n + 1 (L)
+)Nếu m = 2 => C2nH4n + 2 ( ankan)

Đáp án : A
Hidrocacbon có công thức : (CnH2n+1)m ( điều kiện : H ≤ 2C + 2)
=> 2nm + m ≤ 2nm + 2 => m ≤ 2
Vì số H luôn chẵn với hidrocacbon => m =2 => C2nH4n + 2 ( C2nH2.(2n) + 2)
=>Ankan

Đáp án A
Trong hợp chất hidrocacbon ta luôn có: H ≤ 2C + 2 và số H là số chẵn.
CTĐGN là CnH2n+1 => CTPT có dạng là CknH2kn + k
Mà H ≤ 2C + 2 => 2kn + k ≤ 2.kn + 2 => k ≤ 2
Do số H là số chẵn nên k = 2
Vậy CTPT của M có dạng CknH2kn+2 hay CmH2m+2 => M thuộc dãy đồng đẳng của ankan

Chọn đáp án A
( C n H 2 n + 1 = C 2 n H 2 . 2 n + 2 )
là đồng đẳng ankan.
Với tính chất của thi trắc nghiệm ta có thể thử với ankan C2H6 thì CTĐGN nhất là CH3 có dạng C n H 2 n + 1

Đáp án D.
Vì k = 1,67 suy ra X chỉ có thể là anken và ankin
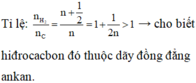
Đáp án A