Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ

Có : AC vuông góc với BD (hình vuông ABCD)
SA vuông góc với BD ( do SA vuông góc với mp ABCD)
=> BD vuông góc với mp SAC...

a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>BC vuông góc AK
mà AK vuông góc SB
nên AK vuông góc (SBC)

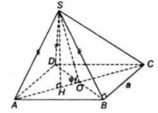
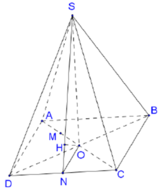
a) Tam giác ABD có AB = AD ( do ABCD là hình thoi)
=> Tam giác ABD cân tại A. Lại có góc A= 60o
=> Tam giác ABD đều.
Lại có; SA = SB = SD nên hình chóp S.ABD là hình chóp đều.
* Gọi H là tâm của tam giác ABD
=>SH ⊥ (ABD)
*Gọi O là giao điểm của AC và BD.
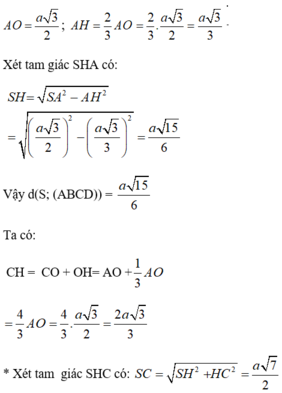

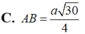
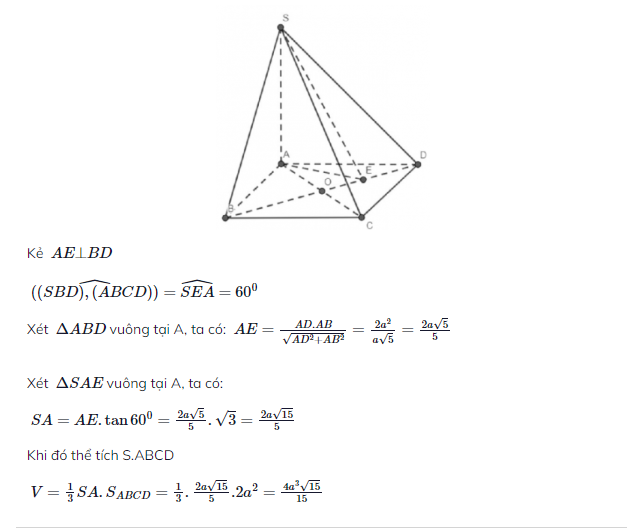
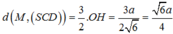
Câu 1:
\(\left(2x+1\right)\left(x^2-2x+3\right)=2x^3-4x^2+6x+x^2-2x+3\)
\(=2x^3-3x^2+4x+3\)
\(\Rightarrow\left[\left(2x+1\right)\left(x^2-2x+3\right)\right]'=6x^2-6x+4\) \(\Rightarrow a+b+c=6-6+4=4\)
Câu 2:
\(v\left(t\right)=s'\left(t\right)=-t^3+9t^2-2\)
\(a\left(t\right)=v'\left(t\right)=-3t^2+18t\)
\(a'\left(t\right)=-6t+18=0\Rightarrow t=3\)
\(\Rightarrow\) vật đạt gia tốc lớn nhất sau 3s kể từ khi chuyển động
Câu 3:
\(y'=x^2-6x-9\)
Gọi tiếp tuyến d' tại \(M\left(x_0;y_0\right)\) có pt \(y=\left(x_0^2-6x_0-9\right)\left(x-x_0\right)+y_0\)
Do \(d//d'\Rightarrow x_0^2-6x_0-9=3\Rightarrow x_0^2-6x_0-12=0\)
\(\Rightarrow\left\{{}\begin{matrix}x_0=3+\sqrt{21}\\x_0=3-\sqrt{21}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}y_0=...\\y_0=...\end{matrix}\right.\) \(\Rightarrow\) pttt
Có vẻ bạn chép sai đề, tiếp tuyến quá xấu
Câu 4:
Ta có: \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\)
\(BD\perp AC\) (tính chất hình thoi)
\(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp SI\)
b/ \(\left(SBD\right)\cap\left(ABCD\right)=BD\); mà \(\left(SAC\right)\perp BD\)
\(\Rightarrow\widehat{SIA}\) là góc giữa (SBD) và (ABCD)
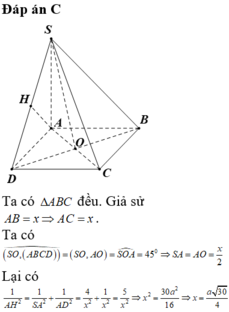
Đặt \(AB=x\); do \(\widehat{ABC}=60^0\Rightarrow\Delta ABC\) đều \(\Rightarrow AC=x\)
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD) \(\Rightarrow\widehat{SCA}=45^0\)
\(\Rightarrow SA=AC.tan\widehat{SCA}=x.1=x\)
\(AI=\frac{1}{2}AC=\frac{x}{2}\Rightarrow tan\widehat{SIA}=\frac{SA}{AI}=\frac{x}{\frac{x}{2}}=2\)
\(\Rightarrow\widehat{SIA}\approx63^026'\)