NT
7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
8 tháng 3 2022
Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=30cm\)
Chu vi tam giác ABC là
AB + AC + BC = 72 cm
AH
Akai Haruma
Giáo viên
6 tháng 7 2024
Lời giải:
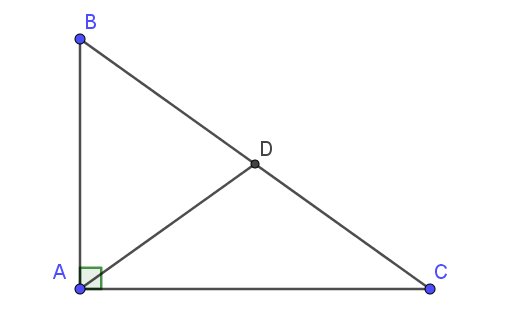
$AD$ là đường trung tuyến ứng với cạnh huyền $BC$
$\Rightarrow AD=\frac{BC}{2}$
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{18^2+24^2}=30$ (cm)
$\Rightarrow AD=30:2=15$ (cm)
8 tháng 2 2020
cho tam giác ABC vuông tại A tính cạnh BC trong các trường hợp sau:
Áp dụng định lý Py-ta-go trong tam giác ABC vuông tại A: BC^2 = AB^2 + AC^2
Thay vào từng trường hợp thì
a, AB=8cm, AC=6cm
=>BC^2=8^2+6^2=100
=>BC=10 cm
b, AB=18cm, AC=24cm
=>BC^2=18^2 + 24^2 = 900
=>BC=30 cm
c, AB=5cm, AC=12cm
=>BC^2= 5^2 + 12^2 =169
=>BC=13 cm
d, AB=12cm. AC=16cm
=>BC^2= 12^2 + 16^2 = 400
=>BC=20 cm
CM
8 tháng 2 2020
tam giác ABC vuông tại A (gt)
=> AB^2 + AC^2 = BC^2 (đl Pytago) (1)
a, AB=8cm, AC=6cm và (1)
=> BC^2 = 8^2 + 6^2
=> BC^2 = 100
=> BC = 10 do BC > 0
b, AB=18cm, AC=24cm và (1)
=> BC^2 = 18^2 + 24^2
=> BC^2 = 900
=> BC = 30 do BC > 0
c, AB=5cm, AC=12cm
=> BC^2 = 5^2 + 12^2
=> BC^2 = 169
=> BC = 13 do BC > 0
d, AB=12cm. AC=16cm
=> BC^2 = 12^2 + 16^2
=> BC^2 =400
=> BC = 20 do BC >0
1 tháng 1 2016
Ta có \(\frac{AB}{AC}=\frac{7}{24}\Rightarrow\frac{AB}{7}=\frac{AC}{24}\)
\(\Rightarrow\frac{AB^2}{49}=\frac{AC^2}{576}=\frac{AB^2+AC^2}{49+576}=\frac{BC^2}{625}\)
\(\Rightarrow\frac{AB}{7}=\frac{AC}{24}=\frac{BC}{25}=\frac{112}{56}=2\)
\(\Rightarrow\) AB = 14 cm; AC = 48 cm; BC = 50 cm
Áp dụng định lý Py-ta-go vào tam giác ABC ta có:
\(AB^2+AC^2=BC^2\)
\(18^2+24^2=BC^2\)
\(324+576=BC^2\)
\(BC^2=900=30^2\)
\(\Rightarrow BC=30\left(cm\right)\)
chu vi tam giác ABC là 30+18+24=72(cm)
vậy ...
sao tính được