
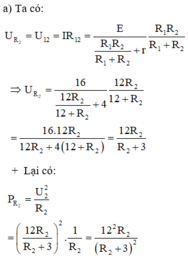
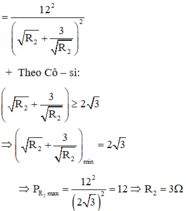
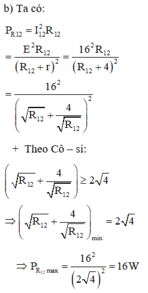

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

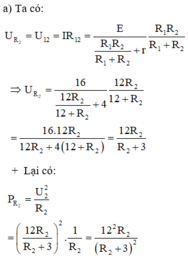
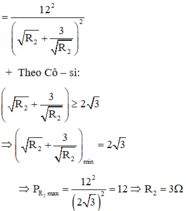
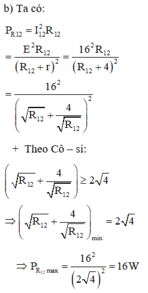


Chọn: C
Hướng dẫn:
- Điện trở mạch ngoài là
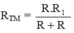
- Xem hướng dẫn câu 2.36: Khi công suất tiêu thụ mạch ngoài lớn nhất thì R TM = r = 2 (Ω).

Công suất tiêu thụ ở mạch ngoài
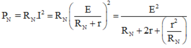
Để công suất mạch ngoài cực đại (Pmax) thì mẫu số của biểu thức trên phải đạt cực tiểu
tức 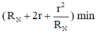
Áp dụng bất đẳng thức Cô-si cho 2 số dương RN và r2/RN
Ta có:
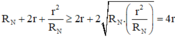
Dấu bằng xảy ra khi RN = r
⇒ Rx = RN – R = r – R = 1,1 – 0,1 = 1Ω
Giá trị cực đại của công suất mạch ngoài:
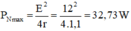

b)Công suất tiêu thụ trên mạch 2:
\(P_2=\left(\dfrac{\xi}{r+R_1+R_2}\right)^2\cdot R_2=\left(\dfrac{24}{4+6+R_2}\right)^2\cdot R_2=\left(\dfrac{24}{10+R_2}\right)^2\cdot R_2\) Áp dụng bđt Cô-sy:
\(P_2=\dfrac{24^2}{(\dfrac{10}{\sqrt{R_2}}+\sqrt{R_2})^2}\le\dfrac{24^2}{10\cdot4}=14,4W\)
Dấu "=" xảy ra\(\Leftrightarrow10=R_2\)
a)Công suất tiêu thụ mạch ngoài:
\(P_N=\left(\dfrac{\xi}{r+R_N}\right)^2\cdot R_N=\dfrac{\xi^2}{\left(\dfrac{r}{\sqrt{R_N}}+\sqrt{R_N}\right)^2}\le\dfrac{\xi^2}{4r}=\dfrac{24^2}{4\cdot4}=36\)
(Bất đẳng thức Cô-sy)
Dấu "=" xảy ra\(\Leftrightarrow r=R_N=4\Omega\)
\(\Rightarrow\dfrac{1}{4}=\dfrac{1}{6}+\dfrac{1}{R_2}\Rightarrow R_2=12\Omega\)