Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1: Người ta muốn mắc dây điện từ một trạm biến áp A đến một khu dân cư B được xây dựng nằm cách xa nhau tại hai bờ của một con sông d. Vị trí trên bờ sông để cắm cột mắc dây C sao cho số mét dây phải dùng là ngắn nhất là:
A. Vị trí cắm cột C là chân đường vuông góc hạ từ trạm biến áp A đến bờ sông d.
B. Vị trí cắm cột C là chân đường vuông góc hạ từ một vị trí B của khu dân cư đến bờ sông d.
C. Vị trí cắm cột C là giao điểm của AB và bờ sông d.
D. Vị trí cắm cột C bất kì trên bờ sông d.

Mọi người làm nhanh jup mik nhé, ai có đáp án sẽ k luôn. Kamsa =)

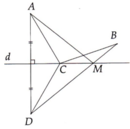
Lấy D là điểm đối xứng, với A qua d. Theo tính chất đường trung trực: CA = CD.
Do đó CA + CB = CD + CB.
Gọi M là giao điểm của BD và d.
Nếu C không trùng với M thì xét tam giác BCD, ta có: CB + CD > BD hay CA + CB > BD (1).
Nếu C trùng với M thì:
CA + CB = MA + MB = MD + MB = BD (2).
So sánh (1) và (2) ta thấy điểm C trùng M hay C là giao điểm của BD và d thì giá trị của tổng CA + CB là nhỏ nhất.
Chú ý: Điểm C tìm được ở vị trí M như vậy là điểm duy nhất. Thật vậy, nếu lấy E đối xứng với B qua d thì AE vẫn cắt d ở M đúng vị trí mà BD cắt d.

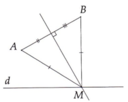
Vì điểm M cách đều hai điểm A và B nên M thuộc đường trung trực của đoạn thẳng AB.
Vậy điểm M là giao điểm của đường thẳng d với đường trung trực của AB.

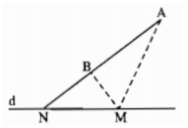
Vì AB không song song với d nên AB cắt d tại N.
Với điểm M bất kỳ thuộc d mà M không trùng với N thì ta có tam giác MAB.
Theo hệ quả bất đẳng thức tam giác ta có:
|MA−MB| < AB
Khi M ≡ N thì
|MA−MB|= AB
Vậy |MA−MB| lớn nhất là bằng AB, khi đó M ≡ N là giao điểm của hai đường thẳng d và AB.
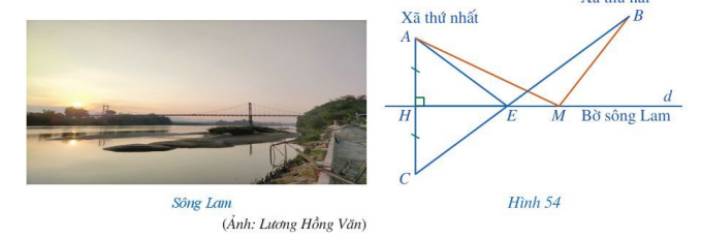
Ta có: HA = HC, \(EH \bot AC\). Vậy EH là đường trung trực của AC nên EA = EC (tính chất đường trung trực của đoạn thẳng).
Tương tự ta có: MH là đường trung trực của AC nên MA = MC.
Xét tam giác MBC: \(BC < MB + MC\)(Trong một tam giác, tổng của hai cạnh luôn lớn hơn độ dài cạnh còn lại).
Ta có:
\(BC < MB + MC = MB + MA\). (1)
Ba điểm B, E, C thẳng hàng nên \(EB + EC = BC\). (2)
Thay (2) vào (1) ta được: \(\begin{array}{l}BC < MB + MA\\EB + EC < MA + MB\end{array}\)
Mà EA = EC nên \(EA + EB < MA + MB\). Vậy bạn Nam nói đúng và khi đó để tổng khoảng cách từ hai xã đến chân cầu là nhỏ nhất thì E là vị trí của cây cầu.