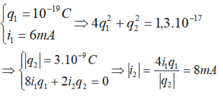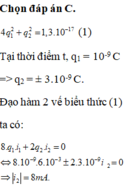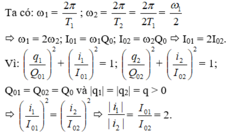Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
Cho \(q_1=10^{-9}C\) và \(i_1=6mA\) và \(4q_1^2+q^2_2=1,3.10^{-17}\left(1\right)\)
Thay \(q_1=10^{-9}C\) vào \(\left(1\right)\) ta có:
\(4q^2_1+q_2^2=1,3.10^{-17}\left(1\right)\Rightarrow q_2=3.10^{-9}C\)
\(4q_1^2+q^2_2=1,3.10^{-17}\) lấy đạo hàm 2 vế theo thời gian \(t\)
\(\Rightarrow8q_1i_1+2q_2i_2=0\left(2\right)\)
Thay \(q_1=10^{-9}C\) và \(i_1=6mA\) và \(q_2=3.10^{-9}C\) vào \(\left(2\right)\) ta có:
\(8q_1i_1+2q_2i_2=0\Rightarrow i_2=8mA\)
Vậy ta chọn \(C.\)
Chú ý: dòng điện tức thời \(i = \frac{dq(t)}{dt} = q(t)'\)
\(4q_1(t)^2+q_2(t)^2 = 1,3.10^{-17} .(1)\)
Lấy đạo hàm 2 vễ phương trình (1). Chú ý \((q(t)^n)' = n.q(t)^{n-1}.q(t)'\)
=> \(4.2.q_1(t).q_1(t)' + 2.q_2(t).q_2(t)' = 0\)
=> \(8q_1.i_1 + 2q_2i_2 = 0.(2)\)
Tại thời điểm t có \(q_1 = 10^{-9}C\) . Thay vào \((1)\) => \(q_2 =\sqrt{ 1,3.10^{-17} - 4.10^{-18}} = 3.10^{-9} C.\)
Thay \(q_1 = 10^{-9}C;i_1 = 6mA; q_2 = 3.10^{-9}C \) vào \((2)\) ta được \(i_2 = -8mA.\)
=> Cường độ dòng thứ hai là 8mA. (độ lớn)
Chọn đáp án. C. 8mA

Đáp án A
Vì T 2 = 2 T 1 → ω 1 = 2 ω 2 ( 1 ) nên ta có cường độ dòng cực đại có mối quan hệ sau: I 01 = ω 1 Q 01 ; I 02 = ω 02 Q 02 .từ (1) suy ra I 01 = 2 I 02 ( 2 ) .Từ biểu thức của q = Q 0 c os ω t → i = − I 0 sin ω t ,ta suy ra công thức độc lập với thời gian: i 1 2 I 2 01 + q 2 Q 01 2 = 1 ; i 2 2 I 2 02 + q 2 Q 2 02 = 1 , từ đây suy ra được i 1 i 2 = I 01 I 02 = 2