Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

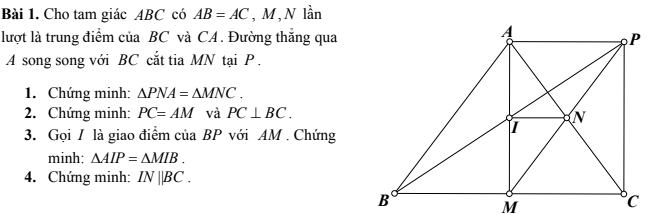
a) Xét tg ABC có AB=AC(gt)
=> tg ABC cân tại A=> B=C
Cách 1( tính chất Tg cân)
ta lại có AM là đường trung tuyến
tg ABC là tg cân => AM là dg cao => AH vg góc vs BC
Cách 2
Xét tg AHB và tg AHC có AH chung
AB=AC( tg ABC cân]
BH=HC( H td BC)
=> tg AHB=tg AHC ( c.c.c)=> AHB=AHC( hai góc bằng nhau)
Mà BHC= 180 độ=> AHB=AHC=180/2=90 độ
=>AH vg góc với BC
b)Ta có CP vg góc với BC (gt)
MN vg góc với BC( N là chân dg vuông góc)
=> MN// CP( từ vg góc đến song song)
Xét tg MCP và tg PNM có:
IMN=IPC( MN//CP; slt)
MN=CP( gt)
MP chung
=>tg MCP=Tg PMN (c.g.c)
C) Xét tg MIN và tg PIC có
IMN=IPC( MN//PC; slt]
MN=CP( gt)
MNI=IPC( MN//PC; slt)
=> tg MIN=tg PIC ( g.c.g)
=>NI=IC( 2 cạnh t/ứ)

1: Xét ΔABC có AB=AC
nên ΔABC cân tại A
Suy ra: \(\widehat{ABC}=\widehat{ACB}\)
Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
Do đó: ΔABH=ΔACH
Suy ra: \(\widehat{AHB}=\widehat{AHC}\)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
Do đó: AH\(\perp\)BC

bài 2
1)
/2x-7/+\(\dfrac{1}{2}=1\dfrac{1}{2}\)
/2x-7/+\(\dfrac{1}{2}=\dfrac{3}{2}\)
/2x-7/=1
=> 2x-7=1 hoặc -2x+7 =1
2x=8 hoặc -2x=-6
x=4 hoặc x=3
Bài 1:
1: Ta có: \(A=\left(-1\right)^3\cdot\left(-\dfrac{7}{8}\right)^3\cdot\left(-\dfrac{2}{7}\right)^2\cdot\left(-7\right)\cdot\left(-\dfrac{1}{14}\right)\)
\(=\dfrac{7^3}{8^3}\cdot\dfrac{4}{49}\cdot\dfrac{1}{2}\)
\(=\dfrac{343}{512}\cdot\dfrac{2}{49}\)
\(=\dfrac{7}{256}\)

Lời giải:
$4+(y-1)^2\geq 4\Rightarrow \frac{8}{4+(y-1)^2}\leq 2$
Mặt khác, áp dụng BĐT $|a|+|b|\geq |a+b|$ ta có:
$|x-1|+|x-3|=|x-1|+|3-x|\geq |x-1+3-x|=2$
$\Rightarrow |x-1|+|x-2|+|x-3|\geq 2+|x-2|\geq 2$
Vậy $\frac{8}{4+(y-1)^2}\leq 2\leq |x-1|+|x-2|+|x-3|$
Dấu "=" xảy ra khi:
\(\left\{\begin{matrix} (y-1)^2=0\\ (x-1)(3-x)\geq 0\\ x-2=0\end{matrix}\right.\Leftrightarrow y=1; x=2\)

Áp dụng t/c dtsbn:
\(a+b+c=\dfrac{c}{a+b+1}=\dfrac{a}{b+c+2}=\dfrac{b}{a+c-3}=\dfrac{a+b+c}{2a+2b+2c}=\dfrac{1}{2}\\ \Rightarrow\left\{{}\begin{matrix}a+b+c=\dfrac{1}{2}\\2c=a+b+1\\2a=b+c+2\\2b=a+c-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a+b+c+1=3c\\a+b+c+2=3a\\a+b+c-3=3b\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3c=\dfrac{3}{2}\\3a=\dfrac{5}{2}\\3b=-\dfrac{5}{2}\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}c=\dfrac{1}{2}\\a=\dfrac{5}{6}\\b=-\dfrac{5}{6}\end{matrix}\right.\)


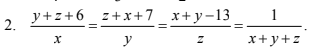
 (
(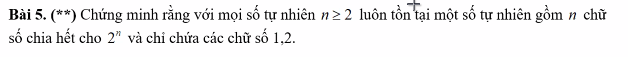
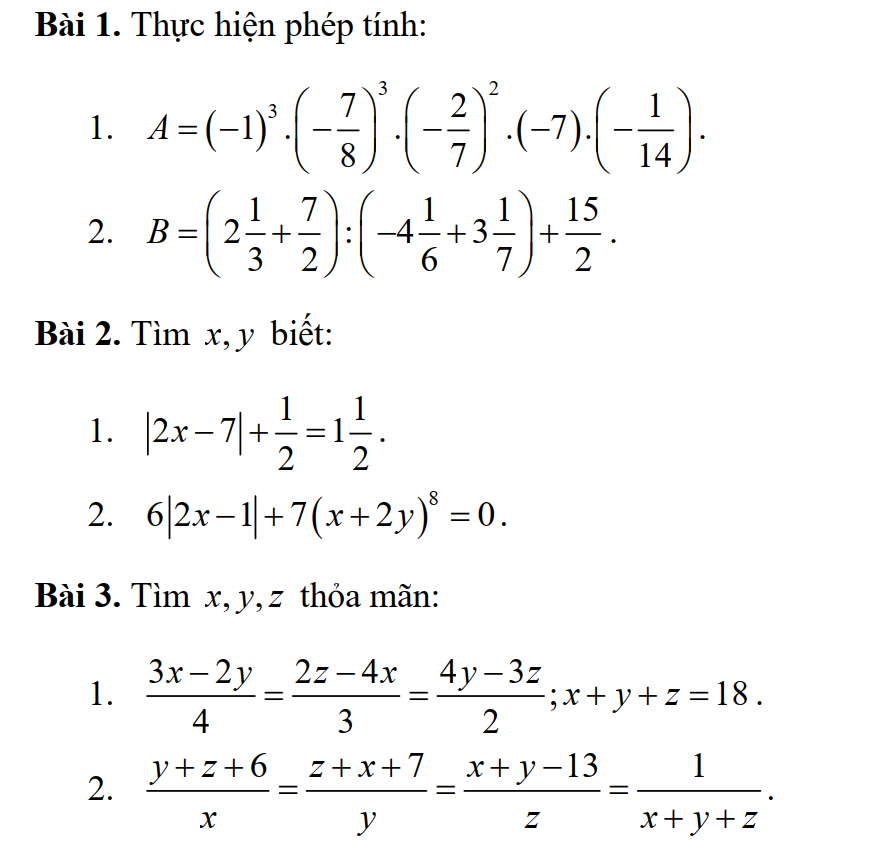
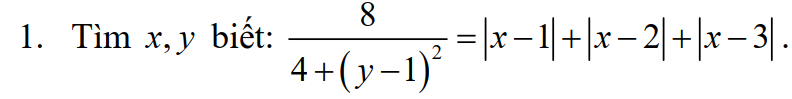
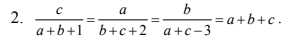 tìm a, b, c
tìm a, b, c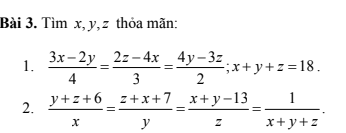
4: Ta có:ΔAIP=ΔMIB
nên IA=IM
hay I là trung điểm của AM
Xét ΔAMC có
I là trung điểm của AM
N là trung điểm của AC
Do đó: IN là đường trung bình của ΔAMC
Suy ra: IN//MC
hay IN//BC
Câu 4 Ta có xét tg PBM có PN=MN( tg PNA=tg MNC)
PI=BI( tg AIP= tgMIB)
=> IN là đường trung bình tg PBM
=>IN//BM <=> IN//BC