Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có bao nhiêu số tự nhiên có tính chất:
a. Là số chẵn và có hai chữ số (không nhất thiết khác nhau).
KQ: \(5\cdot9=45\) (số)
b. Là số lẻ và có hai chữ số (không nhất thiết khác nhau).
KQ: \(5\cdot9=45\) (số)
c. Là số lẻ và có hai chữ số khác nhau.
KQ: \(5\cdot8=40\) (số)
d. Là số chẵn và có hai chữ số khác nhau.
KQ: \(9+4\cdot8=41\) (số)

Có 5 cách chọn chữ số hàngđơn vị là lẻ.
Có 9 cách chọn chữ số hàng chục.
Vậy có 5 × 9 = 45 số lẻ gồm hai chữ số (có thể giống nhau).

Số các số chẵn có hai chữ số, tận cùng bằng 0 là 9.
Để tạo nên số chẵn không chẵn chục, ta chọn chữ số hàng đơn vị khác 0. Có 4 cách chọn. Tiếp theo chọn chữ số hàng chục. Có 8 cách chọn. Vậytheo quy tắc cộng và quy tắc nhân, ta có 9 + 8 × 4 = 41 số chẵn gồm hai chữ số khác nhau.

Chọn B
Gọi số cần tìm là : ![]() a
5
chẵn và trong số luôn có mặt số 0.
a
5
chẵn và trong số luôn có mặt số 0.
Số cần tìm được chọn từ một trong các trường hợp :
Trường hợp 1 : a 5 = 0 có 5 cách chọn.
Khi đó ![]() cách chọn. Suy ra có :
A
9
4
(số).
cách chọn. Suy ra có :
A
9
4
(số).
Trường hợp 2 : ![]() có 4 cách chọn.
có 4 cách chọn.
Chữ số 0 có 3 cách chọn vị trí ![]() cách chọn 3 số cho 3 vị trí còn lại.
cách chọn 3 số cho 3 vị trí còn lại.
Suy ra có : 4.3. A 8 3 (số).
Vậy ta có ![]() thỏa mãn yêu cầu bài toán.
thỏa mãn yêu cầu bài toán.

a) TH1 : Xét số thỏa yêu cầu kể cả chữ số đầu tiên bên trái =0
Chọn 3 chữ số lẻ có C35 cách
Chọn 3 chữ số chẵn có C35 cách
Sắp xếp 6 chữ số này có 6! cách
Vậy có C35 . C35 . 6! số
TH2 : Xét số có 6 chữ số thỏa mãn mà chữ số đầu tiên bên trái =0
Chọn 3 chữ số lẻ có C35 cách
Chọn 2 chữ số chẵn có C24 cách
Sắp xếp 5 chữ số có 5! cách
Vậy có C35 . C24 . 5! số
Vậy có C35 .C35. 6! - C35.C24.5! số tự nhiên gồm 6 chữ số khác nhau trong đó có 3 chữ số chẵn 3 chữ số lẻ

Gọi tập hợp E = {0,1,2,3,4,5}
c) Số tự nhiên có 3 chữ số có dạng
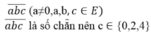
Có ba cách chọn chữ số c ( vì c ∈ {0,2,4}).
Ứng với mỗi cách chọn c , có 6 cách chọn chữ số b (vì b ∈ E)
ứng với mỗi cách chọn c, b có 5 cách chọn chữ số a (vì a ∈ E và a≠ 0)
Áp dụng quy tắc nhân ta có 3*6*5 = 90 số có 3 chữ số.
Vì vậy đáp án là B


Có 5 cách chọn chữ số hàng đơn vị là số chẵn.
Có 9 cách chọn chữ số hàng chục
Theo quy tắc nhân, có 5 × 9 = 45 số chẵn gồm 2 chữ số