Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Gọi số cần tìm là : ![]() a
5
chẵn và trong số luôn có mặt số 0.
a
5
chẵn và trong số luôn có mặt số 0.
Số cần tìm được chọn từ một trong các trường hợp :
Trường hợp 1 : a 5 = 0 có 5 cách chọn.
Khi đó ![]() cách chọn. Suy ra có :
A
9
4
(số).
cách chọn. Suy ra có :
A
9
4
(số).
Trường hợp 2 : ![]() có 4 cách chọn.
có 4 cách chọn.
Chữ số 0 có 3 cách chọn vị trí ![]() cách chọn 3 số cho 3 vị trí còn lại.
cách chọn 3 số cho 3 vị trí còn lại.
Suy ra có : 4.3. A 8 3 (số).
Vậy ta có ![]() thỏa mãn yêu cầu bài toán.
thỏa mãn yêu cầu bài toán.

Gọi số cần tìm có dạng a b c d ¯ với a , b , c , d ∈ A = 1 , 5 , 6 , 7 .
Vì số cần tìm có 4 chữ số không nhất thiết khác nhau nên:
a được chọn từ tập A (có 4 phần tử) nên có 4 cách chọn.
b được chọn từ tập A (có 4 phần tử) nên có 4 cách chọn.
c được chọn từ tập A (có 4 phần tử) nên có 4 cách chọn.
d được chọn từ tập A (có 4 phần tử) nên có 4 cách chọn.
Như vậy, ta có 4.4.4.4 = 256 số cần tìm.
Chọn đáp án B.

Gọi số cần tìm có dạng a b c d ¯ với a , b , c , d ∈ A = 1 , 5 , 6 , 7 .
Vì số cần tìm có 4 chữ số không nhất thiết khác nhau nên:
· a được chọn từ tập A (có 4 phần tử) nên có 4 cách chọn.
· b được chọn từ tập A (có 4 phần tử) nên có 4 cách chọn.
· c được chọn từ tập A (có 4 phần tử) nên có 4 cách chọn.
· d được chọn từ tập A (có 4 phần tử) nên có 4 cách chọn.
Như vậy, ta có 4.4.4.4 = 256 số cần tìm.
Chọn đáp án B.

Các chữ số được đặt trong các ô trống.
| . | . | . | . |
TH1: Số cần lập có chữ số 0:
Đưa 0 vào 3 cách
Đưa 1 vào 3 cách
Đưa 3 vào 2 cách
Lấy 1 số bất kì ô còn lại : 7 cách
=> TH1 có 126 số
TH2: Số cần lập không có chữ số 0:
Đưa 1 vào 4 cách
Đưa 3 vào 3 cách
Lấy 2 số bất kì đưa vào 2 ô còn lại : \(A^2_7\) cách
=> TH2 có 504 số
Vậy lập được tất cả 504 + 126 = 630 số

+ Trước tiên ta đếm số các số tự nhiên có bốn chữ số khác nhau từ các chữ số đã cho.
Gọi số có 4 chữ số là 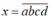
Có 5 cách chọn a(vì a khác 0); khi đó có ![]() cách chọn bcd từ 5 số còn lại.
cách chọn bcd từ 5 số còn lại.
Theo quy tắc nhân có: ![]() số.
số.
+ Tiếp theo, số các số tự nhiên có bốn chữ số khác nhau từ các chữ số đã cho mà không có mặt chữ số 1
Gọi số có 4 chữ số là
Có 4 cách chọn a(vì a khác 0); khi đó có ![]() cách chọn bcd từ 4 số còn lại.
cách chọn bcd từ 4 số còn lại.
Theo quy tắc nhân có ![]() số
số
Vậy số các số tự nhiên có bốn chữ số khác nhau mà nhất thiết phải có mặt số 1 là:
300 – 96 = 204.
Chọn A.

3:
Ta sẽ chia M ra làm 3 nhóm
Nhóm 1: \(A=\left\{0;3;6\right\}\)
Nhóm 2: \(B=\left\{1;4;7\right\}\)
Nhóm 3: \(C=\left\{2;5;8\right\}\)
TH1: 1 số A,1 số B, 1 số C
*Nếu số ở A chọn là số 0 thì sẽ có 3*3*2*2*1=36 cách
*Nếu số A chọn khác 0 thì sẽ là 2*3*3*3!=108 cách
=>Có 108+36=144 cách
TH2: 3 số A
=>Có 2*2*1=4 số
TH3: 3 số B
=>Có 3!=6 số
TH4: 3 số C
=>Có 3!=6 số
=>Có 144+4+6+6=148+12=160 số


Gọi số tự nhiên đó là `\overline{abcdefg}`
`(a,b,c,d,e,f,g in {0;1;2;3;4;5;6;7;8;9} ; a \ne 0 ; a ne b ne c ne d ne e ne f ne g)`
`***` Tất cả số có `7` chữ số khác nhau là: `9. A_9 ^6` số
`***` Xét TH số có `7` chữ số khác nhau không có mặt `2` chữ số `1;2` có: `7.A_7 ^6` số
`=>` Có `9.A_9 ^6 -7.A_7 ^6 =509040` số có `7` chữ số khác nhau và nhất thiết có mặt `2` chữ số `1;2`
Cứ coi số 1;2 như 1 số
\(\overline{abcdef}\)
Ta sẽ chọn ra số có 6 chữ số từ tập {0;{1;2};3;4;5;6;7;8;9}
=>Có \(A^6_9=60480\left(số\right)\) kể cả số bắt đầu bằng 0
Ta sẽ loại trường hợp bắt đầu bằng 0
a=0 thì có 1 cách chọn
số cách chọn cho 5 chữ số còn lại là:\(A^5_8=6720\left(số\right)\)
=>Có 60480-6720=53760(số)