K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 8 2016
Tam giác DKE có:
+
+
=900 (tổng ba góc trong của tam giác).
+800 +400=1800
=1800 -1200=
Nên
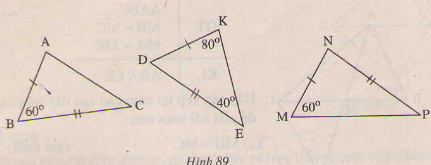
∆ ABC và ∆KDE có:
AB=KD(gt)
=
=600và BE= ED(gt)
Do đó ∆ABC= ∆KDE(c.g.c)
Tam giác MNP không có góc xem giữa hai cạnh tam giác KDE ha ABC nên không bằng hai tam giác còn lại .
12 tháng 8 2016
- Tam giác DKE có: ∠D + ∠K + ∠E = 1800 (tổng ba góc trong của tam giác).
hay ∠D + +800 +400 = 1800
⇒∠D = 1800 -1200 = 600
Xét ∆ ABC và ∆KDE có:
AB = KD(gt)
∠B = ∠D ( cùng = 600 )
và BE = ED (gt)
Do đó ∆ABC= ∆KDE (c.g.c)
- Tam giác MNP không có góc xem giữa hai cạnh tam giác KDE ha ABC nên không bằng hai tam giác còn lại .
19 tháng 10 2015
A B C H
Gọi tam giác đều đã cho là tam giác ABC.
Kẻ đường cao AH . Tam giác ABC đều nên AH là đường trung tuyến => H là trung điểm của BC => BH = BC/2 = AB/2
Áp dụng ĐL Pi ta go trong tam giác vuông ABH có: AH2 = AB2 - BH2 = AB2 - AB2/4 = 3AB2/4 => AH = \(\frac{AB\sqrt{3}}{2}\)
S(ABC) = AH.BC/2 = \(\frac{AB^2\sqrt{3}}{4}=4\sqrt{3}\) => AB2 = 16 => AB = 4 cm
=> Chu vi tam giác đều ABC là: AB .3 = 12 cm
+) Tổng quát : Kí hiệu a là cạnh của tam giác đều => S tam giác đều = \(\frac{a^2\sqrt{3}}{4}\) (*)
+) Chu vi lục giác đều bằng 12 cm => cạnh của lục giác đều là: 12 : 6 = 2 cm
Chia lục giác đều thành 6 tam giác đều bằng nhau có cạnh bằng cạnh của lục giác đó
Áp dụng công thức (*) => Diện tích 1 tam giác = \(\frac{4\sqrt{3}}{4}=\sqrt{3}\) cm2
Diện tích lục giác = 6 x Diện tích 1 tam giác = \(6\sqrt{3}\) cm2
ĐS:...
4 tháng 5 2020
AD định lí tổng 3 góc trong tam giác ABD ta có
góc BAD +gócB =130 độ (1)
Vì ADC và BAD là 2 góc kề bù => gócADC=130 độ
AD định lí tổng 3 góc trong tam giác ADC ta có
góc DAC + góc C= 50 độ (2)
Mà góc BAD=góc DAC nên lấy (1)- (2) ta đc
góc B-góc C= 130-50=80 độ
NS
4
BA
26 tháng 3 2016
Ta có : BC = 2 \(\sqrt{2}\)
=> BC = \(\sqrt{4}\)= 2 cm
Lại có : AB = 2cm , AC = 2 cm
=> \(\Delta\)ABC đều
=> góc C = 60\(^o\)
28 tháng 2 2015
Cần 4 điểm
3 điểm tạo tành 1 tam giác lớn và 1 điểm nằm giữa. Nối 3 điểm đỉnh của tam giác lớn với điểm nằm giữa ta sẽ có 4 tam giác
17 tháng 6 2018
A B C D E 112^o M N
Gọi M; N là ....
Ta có : \(DM\perp AB\)\(\Rightarrow\)DM là đường cao \(\Delta ABD\)
\(AM=MB\Rightarrow\)DM là trung tuyến \(\Delta ABD\)
\(\Rightarrow\Delta ABD\)cân tại D
\(\Rightarrow\widehat{BAD}=\widehat{ABD}\)
CM tương tự \(\Rightarrow\Delta AEC\)cân tại E
\(\Rightarrow\widehat{EAC}=\widehat{ACE}\)
Mà \(\widehat{BAD}+\widehat{EAC}+\widehat{DAE}=\widehat{BAC}=112^o\)
\(\Rightarrow\widehat{ABD}+\widehat{ACE}+\widehat{DAE}=112^o\left(1\right)\)
Mặt khác \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^o\)
\(\Leftrightarrow\widehat{ABC}+\widehat{ACB}+112^o=180^o\)
\(\Leftrightarrow\widehat{ABC}+\widehat{ACB}=68^o\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\widehat{DAE}=44^o\)
Vậy ...
6 tháng 3 2016
Ta có tam giác vuông ABH = CAI (c.h-g.n) => BH = AI
Áp dụng Pytago trong tam giác vuông ACI có:
AC² = AI² + IC² hay AC² = BH² + IC²
Đặt AB = AC = a; áp dụng Pytago trong tam giác vuông ABC ta có BC² = 2a²
Vậy BC²/( BH² + CI²) = BC²/ AC² = 2a²/a² = 2
24 hình
mk đếm ko kĩ cho lắm đúng thì tk nha