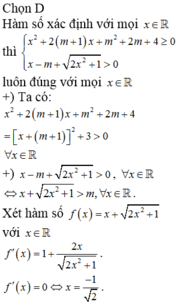Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải + diễn giải
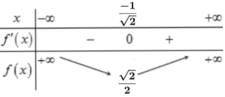
để hàm có cực trị f'(x) phải có nghiệm và đổi dấu qua nghiệm
a) \(y'=3x^2-6x+m\)
xét f(x)= 3x^2 -6x+m
để f(x) là hàm bậc 2 => có nghiệm và đổi dấu qua nghiệm đk cần và đủ \(\Delta>0\)
\(\Leftrightarrow\Delta'=9-3m>0\Rightarrow m< 3\)
Kết luận với m< 3 hàm A(x) luôn có cực trị
b)
\(y'=3x^2+4mx+m\)
\(\Delta'=4m^2-3m>0\Leftrightarrow\left[{}\begin{matrix}m< 0\\m>\dfrac{3}{4}\end{matrix}\right.\)
c)
\(y=\dfrac{x^2-2mx+5}{x-m}\Rightarrow\left\{{}\begin{matrix}x\ne m\\y=\left(x-m\right)+\dfrac{5-m^2}{x-m}\end{matrix}\right.\)
\(y'=1+\dfrac{m^2-5}{\left(x-m\right)^2}\)
\(y'=0\Leftrightarrow\left(x-m\right)^2+m^2-5=0\Rightarrow5-m^2>0\Rightarrow-\sqrt{5}< m< \sqrt{5}\)

a) y = f(x) = x3 – 3mx2 + 3(2m-1)x + 1
Tập xác định: D = R
y’= 3x2 -6mx + 3(2m-1) = 3(x2 – 2mx + 2m – 1)
Hàm số đồng biến trên D = R ⇔ y’ ≥ 0, ∀x ∈ R
⇔ x2 – 2mx + 2m - 1≥0, ∀x ∈ R
⇔ Δ’ = m2 – 2m + 1 = (m-1)2 ≤ 0 ⇔ m =1
b) Hàm số có một cực đại và một cực tiểu
⇔ phương trình y’= 0 có hai nghiệm phân biệt
⇔ (m-1)2 > 0 ⇔ m≠1
c) f’’(x) = 6x – 6m > 6x
⇔ -6m > 0 ⇔ m < 0

a) y′=3x+2(m+3)x=x[3x+2(m+3)];y′=0⇔x1=0y′=3x2+2(m+3)x=x[3x+2(m+3)];y′=0⇔x1=0
hoặc x2=−2m+63x2=−2m+63
Xảy ra hai trường hợp đối với dấu của y':
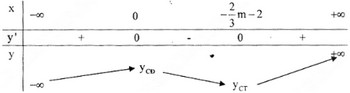
Rõ ràng, để hàm số có điểm cực đại tại x = -1 ta phải có
x2=−2m+63=−1⇔m=−32x2=−2m+63=−1⇔m=−32
(Chú ý : trường hợp x1 = x2 thì hàm số không có cực trị).
b) (Cm) cắt Ox tại x = -2 ⇔ -8 + 4(m + 3) + 1 - m = 0 ⇔ m=−53m=−53

a) y= -x4 + 2mx2 – 2m + 1(Cm). Tập xác định: D = R
y ‘ = -4x3 + 4mx = -4x (x2 – m)
- Với m ≤ 0 thì y’ có một nghiệm x = 0 và đổi dấu + sang – khi qua nghiệm này. Do đó hàm số có một cực đại là x = 0

Do đó, hàm số có 2 cực trị tại x = ± √m và có một cực tiểu tại x = 0
b) Phương trình -x4 + 2mx2 – 2m + 1 = 0 luôn có nghiệm x = ± 1 với mọi m nên (Cm) luôn cắt trục hoành.
c) Theo lời giải câu a, ta thấy ngay:
với m > 0 thì đồ thị (Cm) có cực đại và cực tiểu.

a) Tập xác định: D = R\{m}
Hàm số đồng biến trên từng khoảng (−∞;m),(m;+∞)(−∞;m),(m;+∞)khi và chỉ khi:
y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2
b) Tập xác định: D = R\{m}
Hàm số nghịch biến trên từng khoảng khi và chỉ khi:
y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0
[m<1m>4[m<1m>4
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3
d) Tập xác định: D = R
Hàm số đồng biến trên R khi và chỉ khi:
y′=3x2−4mx+12≥0⇔′=4m2−36≤0⇔m2≤9⇔−3≤m≤3

Phương trình hoành độ giao điểm của đồ thị và đường thẳng là \(-x+m=\frac{x^2-1}{x}\)
\(\Leftrightarrow2x^2-mx-1=0\) (*) (vì x = 0 không là nghiệm của (*))
Vì ac < 0 nên phương trình (*) luôn có 2 nghiệm phân biệt khác không
Do đó đồ thị và đường thẳng luôn cắt nhau tại hai điểm phân biệt :
\(A\left(x_1;-x_1+m\right);B\left(x_2;-x_2+m\right)\)
\(AB=4\Leftrightarrow\sqrt{\left(x_2-x_1\right)^2+\left(-x_2+m+x_1+m\right)^2}=4\)
\(\Leftrightarrow2\left(x_2-x_1\right)^2=16\)
\(\Leftrightarrow\left(x_2+x_1\right)^2-4x_2x_1=8\)
Áp ụng định lý Viet ta có : \(\begin{cases}x_2+x_1=\frac{m}{2}\\x_2x_1=-\frac{1}{2}\end{cases}\)
\(AB=4\Leftrightarrow\frac{m^2}{4}+2=8\Leftrightarrow m=\pm2\sqrt{6}\)
Vậy \(m=\pm2\sqrt{6}\) là giá trị cần tìm

Tập xác định :
Nếu hàm số đạt cực đại tại x = 2 thì y'(2) = 0 ⇔ m2 + 4m + 3 = 0 ⇔ m=-1 hoặc m=-3
- Với m = -1, ta có :
x=0 hoặc x=2.
Ta có bảng biến thiên :
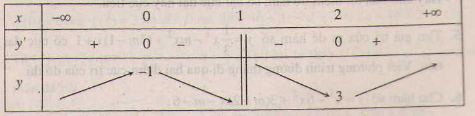
Trường hợp này ta thấy hàm số không đạt cực đại tại x = 2.
- Với m = -3, ta có:
x=2 hoặc x=4
Ta có bản biến thiên :
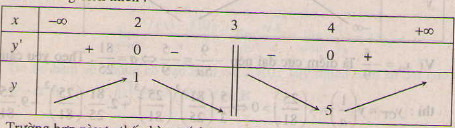
Trường hợp này ta thấy hàm số đạt cực đại tại x = 2.
Vậy m = -3 là giá trị cần tìm.

- Khi \(m=0\Rightarrow y=x-1\) nên hàm số không có cực trị
- Khi \(m\ne0\Rightarrow y'=3mx^2+6mx-\left(m-1\right)\)
hàm số không có cực trị khi và chỉ chỉ y' = 0 không có nghiệm hoặc có nghiệm kép
\(\Leftrightarrow\Delta'=9m^2+3m\left(m-1\right)=12m^2-3m\le0\) \(\Leftrightarrow0\le m\)\(\le\frac{1}{4}\)

1.
Hàm trùng phương có đúng 1 cực trị khi:
TH1: \(a=m=0\)
TH2: \(ab=-m>0\Leftrightarrow m< 0\)
\(\Rightarrow m\le0\)
Đáp án B
2.
\(y'=3\left(x^2+2mx+m^2-1\right)=3\left(x+m+1\right)\left(x+m-1\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}x=-m+1\\x=-m-1\end{matrix}\right.\)
Hàm số có 2 cực trị nằm về 2 phía trục hoành
\(\Leftrightarrow y'\left(-m+1\right).y'\left(-m-1\right)< 0\)
\(\Leftrightarrow\left(3m-2\right)\left(3m+2\right)< 0\Rightarrow-\frac{2}{3}< m< \frac{2}{3}\)
\(\Rightarrow a+2b=-\frac{2}{3}+2.\frac{2}{3}=\frac{2}{3}\)