

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
A ∈ y ⇒ A ( x ; x 3 − 3 x 2 − x + 2 ) d ( A ; Ox)=d(A;Oy) ⇒ x 3 − 3 x 2 − x + 2 = x x 3 − 3 x 2 − x + 2 = − x
Giải hai pt trên ta thấy mỗi pt có 3 nghiệm
Vậy có 6 điểm thỏa mãn yêu cầu đề bài

Đáp án A
Điểm M a ; b thuộc đồ thị (C)
=> b = a − 3 a + 1
⇒ a + b = a + a − 3 a + 1 = a + 4 a + 1 − 1 ≥ a + 1 + 4 a + 1 − 2 ≥ a + 1 + 4 a + 1 − 2 ≥ 4 − 2 = 2
Như vậy tổng khoảng cách từ M tới hai trục tọa độ nhỏ nhất bằng 2 ⇔ a = 1 b = − 1 ⇒ T = − 2

Do tiếp tuyến tại cắt trục tọa độ Ox, Oy lần lượt tại A, B nên tiếp tuyến có hệ số góc k với 
Ta có  nên k = -3
nên k = -3
Khi đó 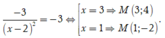
Chọn B.

Đáp án D
y = x − 1 x + 1 C ⇒ M m ; m − 1 m + 1 m ≠ − 1
Tổng khoảng cách từ M đến hai trục tọa độ là d = m + m − 1 m + 1 m ≠ − 1
- Với m = 0 ⇒ d = 1 ⇒ min d ≤ 1 ⇒ Xét sao cho d ≤ 1
⇔ m + m − 1 m + 1 ≤ 1 ⇒ m ≤ 1 m − 1 m + 1 < 1 ⇔ 0 ≤ m ≤ 1
- Với
m ∈ 0 ; 1 ⇒ d = m + 1 − m m + 1 = m 2 + 1 m + 1
Khảo sát hàm số f m = m 2 + 1 m + 1 trên 0 ; 1 ⇒ min 0 ; 1 f m = 2 2 − 2
Khi m = 2 − 1 ⇒ M − 1 + 2 ; 1 − 2