Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có: y ' = x − 1 − x + 3 x − 1 2 = − 4 x − 1 2 .
Tiếp tuyến tại M x 0 ; x 0 + 3 x 0 − 1 ∈ C là:
y = − 4 x 0 − 1 2 x − x 0 + x 0 + 3 x 0 − 1 = − 4 x x 0 − 1 2 + x 0 2 + 6 x 0 − 3 x 0 − 1 2 .
Tiếp tuyến đi qua M x 1 ; 2 x 1 + 1 nên:
2 x 1 + 1 = − 4 x 1 x 0 − 1 2 + x 0 2 + 6 x 0 − 3 x 0 − 1 2
⇔ 2 x 1 + 1 x 0 2 − 2 x 0 + 1 = x 0 2 + 6 x 0 − 3 − 4 x 1 ⇔ 2 x 1 − 1 x 0 2 − 4 x 1 + 2 x 0 + 6 x 1 + 4 = 0 (*)
Qua M x 1 ; 2 x 1 + 1 kẻ được đúng một tiếp tuyến đến đồ thị hàm số (C) nên (*) có nghiệm duy nhất
⇔ Δ ' = 4 x 1 + 2 2 − 2 x 1 − 1 6 x 1 + 4 = 0 ⇔ − 4 x 1 2 + 7 x 1 + 10 = 0 ⇔ x 1 = 7 ± 209 8 .
Vậy có 2 điểm từ đó kẻ được đúng 1 tiếp tuyến đến đồ thị hàm số.


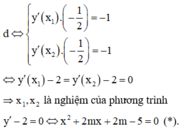
Điều kiện bài toán thỏa mãn (*) có 2 nghiệm phân biệt trái dấu
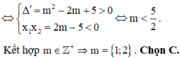

Đáp án C
Phương pháp:
Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
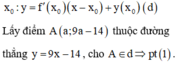
Để từ A kẻ được hai tiếp tuyến đến (C) thì phương trình (1) có 2 nghiệm phân biệt. Tìm điều kiện của a để phương trình có 2 nghiệm phân biệt. Có bao nhiêu giá trị của a thì có bấy nhiêu điểm thỏa mãn yêu cầu bài toán.

Cách giải:
TXĐ : D = R.
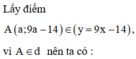
9 a − 14 = 3 x 0 2 − 3 a − x 0 + x 0 3 − 3 x 0 + 2 1
⇔ 9 a − 14 = 3 a x 0 2 − 3 x 0 3 − 3 a + 3 x 0 + x 0 3 − 3 x 0 + 2
⇔ − 2 x 0 3 + 3 a x 0 2 − 12 a + 16 = 0
⇔ x 0 − 2 − 2 x 0 2 + 3 a − 4 x 0 + 6 a − 8 = 0
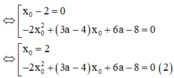
Để qua A kẻ được 2 tiếp tuyến đến đồ thị (C) thì phương trình (1) có 2 nghiệm phân biệt.
TH1 : x 0 = 2 là nghiệm của phương trình (2) ta có :

TH2 : x 0 = 2 không là nghiệm của phương trình (2), khi đó để (1) có 2 nghiệm phân biệt thì (2) có nghiệm kép khác 2.
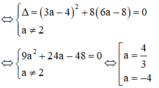
Vậy có 3 giá trị của a thỏa mãn yêu cầu bài toán.
Chú ý và sai lầm: Cần phải làm hết các trường hợp để phương trình (1) có 2 nghiệm, tránh trường hợp thiếu TH1 và chọn nhầm đáp án B.

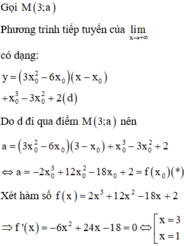




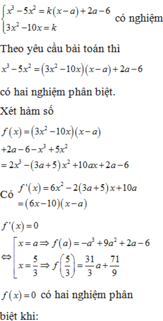
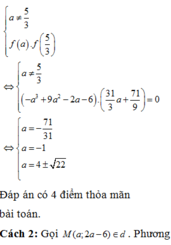

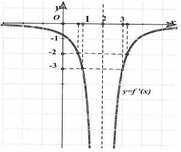


Đáp án đúng : C