Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
$y'=\frac{2x}{\sqrt{2x^2+1}}$
$y'>0\Leftrightarrow 2x>0\Leftrightarrow x>0$ hay $x\in (0;+\infty)$
$y'< 0\Leftrightarrow 2x< 0\Leftrightarrow x\in (-\infty;0)$
Vậy hàm số đồng biến trên $(0;+\infty)$ và nghịch biến trên $(-\infty; 0)$
Đáp án A.

Ghi lại đề bài đi bạn, đề thế này không ai biết nó là gì cả

Chọn D
i) Đúng.
ii) Sai, ví dụ: Xét hàm số
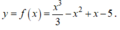
Ta có f ' x = x 2 - 2 x + 1 .
Cho f ' ( x ) ⇔ x = 1 .
Khi đó phương trình f ' ( x ) = 0 có nghiệm x 0 = 1 nhưng đây là nghiệm kép nên không đổi dấu khi qua x 0 .
iii) Sai, vì: Thiếu điều kiện f ' ( x ) = 0 chỉ tại một số hữu hạn điểm.
Vậy có 1 mệnh đề đúng.




\(y=\frac{ax+b}{x+1}\Rightarrow y'=\frac{a-b}{x+1}\)
Hàm đồng biến trên mỗi khoảng xác định khi và chỉ khi \(a>b\)
\(\Rightarrow0< b< a\le20\)
Ứng với mỗi giá trị của b, có \(20-b\) giá trị a tương ứng thỏa mãn
Mà có 19 giá trị của b\(=\left\{1;2;3;...;19\right\}\)
\(\Rightarrow\) Có \(\left(20-1\right)+\left(20-2\right)+...+\left(20-19\right)\) cặp số nguyên
Hay \(20.19-\left(1+2+...+19\right)=190\) cặp