Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có BM/BC=BD/BA
nên MD//AC
=>MM' vuông góc AB
=>M đối xứngM' qua AB
b: Xét tứ giác AMBM' có
D là trung điểm chung của AB và MM'
MA=MB
Do đó: AMBM' là hình thoi

a: ĐKXĐ: x<>2; x<>-3
b: \(P+\dfrac{x^2-4-5-x-3}{\left(x-2\right)\left(x+3\right)}=\dfrac{\left(x-4\right)\left(x+3\right)}{\left(x-2\right)\left(x+3\right)}=\dfrac{x-4}{x-2}\)
c: Để P=-3/4 thì x-4/x-2=-3/4
=>4x-8=-3x+6
=>7x=14
=>x=2(loại)
e: x^2-9=0
=>x=3 (nhận) hoặc x=-3(loại)
Khi x=3 thì \(P=\dfrac{3-4}{3-2}=-1\)

\(\dfrac{x+9}{x^2-9}-\dfrac{3}{x^2+3x}\)
\(=\dfrac{x+9}{\left(x-3\right)\left(x+3\right)}-\dfrac{3}{x\left(x+3\right)}\)
\(=\dfrac{x\left(x+9\right)}{x\left(x-3\right)\left(x+3\right)}-\dfrac{3\left(x-3\right)}{x\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x^2+9x-3x+9}{x\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x^2+6x+9}{x\left(x-3\right)\left(x+3\right)}=\dfrac{\left(x+3\right)^2}{x\left(x-3\right)\left(x+3\right)}=\dfrac{x+3}{x\left(x-3\right)}\)
______________________________________________________
\(\dfrac{x+1}{2x+6}-\dfrac{x-6}{2x^2+6x}\)
\(=\dfrac{x+1}{2\left(x+3\right)}-\dfrac{x-6}{2x\left(x+3\right)}\)
\(=\dfrac{x\left(x+1\right)}{2x\left(x+3\right)}-\dfrac{x-6}{2x\left(x+3\right)}\)
\(=\dfrac{x^2+x-x+6}{2x\left(x+3\right)}=\dfrac{x^2+6}{2x\left(x+3\right)}\)

Tự vẽ hình nha
Vì CO là phân giác góc ACB
CO' là tia phân giác góc ngoài đỉnh C
=> CO vuông góc CO' ( hai tia phân giác của hai góc kề bù vuông góc với nhau )
=> Tam giác COO' vuông tại C
=> OO'2 = CO2 + CO'2
=> OO'2 = 32 + 42
=> OO'2 = 25
=> OO' = 5 ( cm )
Vì S là trung điểm OO'
=> SC là đường trung tuyến ứng với OO' trong tam giác COO'
mà OO' là cạnh huyền
=> SC = 1/2 OO' ( trong tam giác vuông, trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền )
=> SC = 5/2 = 2,5 ( cm )
Chúc bạn học tốt
Vì CO , CO' là tia phân giác
\(\Rightarrow CO\perp CO'\)
\(=90^o\)
\(\Rightarrow\Delta COO'\perp\)
Mặt khác S là trung điểm của OO'
=> CS là đường trung tuyến ứng với OO'
Lại có OO' là cạnh huyền
\(\Rightarrow CS=\frac{1}{2}OO'\)( định lí trong tam giác vuông)
Áp dụng định lí py-ta-go cho tam giác vuông COO' ta có :
Thay các giá trị để tìm SC .

gọi số lớn là a, số nhỏ là b
Theo đề bài ta có:
a + b = 16 (1)
a^2 - b^2 = 32
<=> (a+b)(a-b)=32
<=> 16.(a-b)=32
<=> a-b = 32/16 = 2
<=> a=2+b thế vào (1)
(1) <=> 2+b+b=16
<=> b=7 ; a= 7+2=9
vậy 2 số đó là 7 và 9
k mk nha
gọi số lớn là a, số nhỏ là b
Theo đề bài ta có:
a + b = 16 (1)
\(a^2\) - \(b^2\) = 32
<=> (a+b)(a-b)=32
<=> 16.(a-b)=32
<=> a-b = \(\frac{32}{16}\) = 2
<=> a=2+b thế vào (1)
(1) <=> 2+b+b=16
<=> b=7 ; a= 7+2=9
vậy 2 số đó là 7 và 9
Tk mk nha




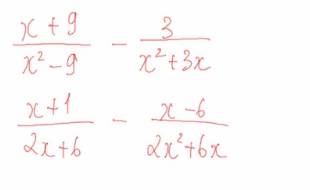
Bạn chớ đăng linh tinh nhé.(Lời khuyên chân thành).