Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ đỏ đến xanh dương có 4 đường chạy khác nhau, từ xanh dương đến xanh lá có 6 cách chọn đường. Như vậy, ứng với mỗi cách lựa chọn đi từ đỏ đến xanh dương sẽ có 6 cách lựa chọn khác nhau để đi từ xanh dương đến xanh lá. Ta có tổng số cách (số đường) để có thể chạy từ đỏ đến xanh lá là: 4 x6 = 24 đường.
Để tồn tại chắc chắn 3 người trên cùng một đường trong suốt cuộc đua cần ít nhất số người là: 24 x 2 + 1= 49 người
Đáp án: B

Ta sẽ chứng minh cần ít nhất 21 người. Thật vậy, nếu có ít nhất 21 người tham gia đường đua thì do có tổng cộng 10 con đường khác nhau nên theo nguyên lí Diriclet tồn tại 1 con đường có từ 3 người tham gia trở lên.
Với trường hợp có 20 người tham gia, ta chỉ ra 1 trường hợp không thỏa mãn:
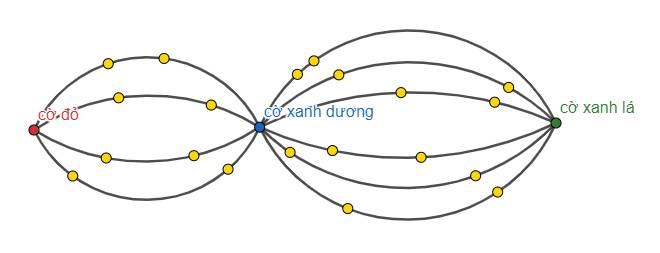
Ta dễ dàng lập những sơ đồ tương tự để chứng minh nếu có \(\le19\) người tham gia thì không đảm bảo điều kiện đề bài.
Như vậy cần có ít nhất 21 người tham gia để đảm bảo điều kiện bài toán được thỏa mãn.

Có 15 quả bóng màu xanh, 13 quả bóng màu đỏ và 17 quả bóng màu trắng => Có 45 kết quả có thể. Các kết quả có thể này là đồng khả năng
a) Có 15 quả bóng màu xanh => Có 15 kết quả thuận lợi cho biến cố C
Vậy \(P(C) = \frac{{15}}{{45}} = \frac{1}{3}\)
b) Có 13 quả bóng màu đỏ => Có 13 kết quả thuận lợi cho biến cố D
Vậy \(P(D) = \frac{{13}}{{45}}\)
c) Có 28 kết quả thuận lợi cho biến cố E
Vậy \(P(E) = \frac{{28}}{{45}}\)

Gọi \(x\) (cây) là số cây viết màu xanh mà An đã mua \(\left(x\inℕ^∗;0< x< 10\right)\)
Vì An mua 10 cây bút xanh và đỏ nên số cây bút đỏ là \(10-x\) (cây)
Do mỗi cây viết màu xanh có giá 12 nghìn đồng nên số tiền An dành ra để mua viết xanh là \(12x\) (nghìn đồng)
Mỗi cây viết màu đỏ có giá 8 nghìn đồng nên số tiền An dành ra để mua viết đỏ là \(8\left(10-x\right)=80-8x\) (nghìn đồng)
Vì An phải trả số tiền là 96 nghìn đồng nên ta có pt
\(12x+80-8x=96\) \(\Leftrightarrow4x=16\) \(\Leftrightarrow x=4\) (nhận)
Vậy An đã mua 4 cây viết xanh và 6 cây viết đỏ.

Giả sử hội trường có a dãy và b là số ghế của mỗi dãy. (a,b∈N∗a,b∈N∗).
Ta có phương trình: ab=500ab=500 và
⇒(a−3)(b+3)=506⇒ab−3b+3a−9=506⇒3(a−b)=15⇒a−b=5⇒a(a−5)=500⇔a=25⇒(a−3)(b+3)=506⇒ab−3b+3a−9=506⇒3(a−b)=15⇒a−b=5⇒a(a−5)=500⇔a=25
Vậy lúc đầu người ta định xếp 2525 dãy ghế.

Để 2 chữ A luôn đứng cạnh nhau thì ta sẽ coi hai chữ đó là cùng 1 chữ, sau đó ta sẽ tính cách xếp các chữ T,H,AA,I,L,N,D vào 7 vị trí trong từ
=>Số cách xếp là \(7!=5040\left(cách\right)\)
Nếu xếp ngẫu nhiên 9 cờ rồi hoán đổi vị trí lần lượt, ta có 9!9! cách xếp.
Thực tế việc hoán đổi vị trí 6 cờ xanh cho nhau, 3 cờ đỏ cho nhau là trùng lặp vì các cờ giống nhau chỉ có 1 cách xếp.
Vậy số cách xếp là:
9!6!.3!=84