

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn A
Số cách để xếp người vào bàn tròn là : 7!=5040(cách)
Để xếp cho hai nữ không ngồi cạnh nhau, trước tiên ta xếp nam trước: 4!=24(cách)
Giữa nam có 5 chỗ trống, số cách để xếp 3 nữ vào 5 chỗ trống là: ![]()
Vậy xác suất để xếp cho hai nữ không ngồi cạnh nhau là: ![]()

Đáp án B
Số phần tử KGM là: 9!. Mà số phần tử của biến cố các học sinh nữ luôn ngồi cạnh nhau là: 3!7!
Xác suất để các học sinh nữ luôn ngồi cạnh nhau là: 3!7! 9! = 1 12

Chọn B.
Phương pháp: Sử dụng hoán vị và quy tắc nhân.
Cách giải: Xếp 12 học sinh vào 12 ghế có 12! cách xếp.
Đánh số ghế như sau:
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Chọn giới tính nam hoặc nữ có 2 cách.
Xếp nam hoặc nữ ngồi vào các ghế 1, 3, 5, 8, 10,12 có 6!= 720 cách.
Xếp các bạn giới tính còn lại vào 6 ghế còn lại có 6!= 720cách.
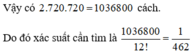

Chọn đáp án A
Kí hiệu Nam: l và Nữ: ¡. Ta có
Có 2 trường hợp Nam, nữ ken kẽ nhau và 4 trường hợp hai bạn Nữ ngồi cạnh nhau.
Trường hợp 1. Nam nữ ngồi xen kẽ nhau gồm:
Nam phía trước: l¡l¡l¡l¡l¡.
Nữ phía trước: ¡l¡l¡l¡l¡l.
Trường hợp 2. Hai bạn nữ ngồi cạnh nhau: l¡¡l¡l¡l¡l Hoặc
l¡l¡¡l¡l¡l. Tương tự ta có thêm 2 trường hợp nữa. Các bước xếp như sau:
B1: Xếp 5 bạn nam. B2: Xếp cặp Tự - Trọng. B3: Xếp các bạn nữ còn lại. Khi đó số kết quả xếp cho 2 trường hợp trên như sau:



Gọi X là biến cố: "Anh A và chị B ngồi cạnh nhau"
Chọn vị trí cho cặp A, B ngồi có 2 cách là: {3,4}, {4,5}
Xếp A, B vào ghế có 2!
Xếp 3 người còn lại vào 3 vị trí còn lại, có 3! cách.


Số phần tử không gian mẫu là: ![]()
Gọi X là biến cố: " Anh A và chị B ngồi cạnh nhau ".
● Chọn vị trí cho cặp A, B ngồi có 2 cách là: ![]()
Xếp A, B vào ghế có 2!
● Xếp 3 người còn lại vào 3 vị trí còn lại, có: 3! cách
Suy ra số phần tử của biến cố: ![]()
Vậy xác suất cần tính P(X) = 1 5
Chọn C.

Đáp án A.
Đặt Ω là không gian mẫu. Ta có n Ω = 2 8 = 256 .
Gọi A là biến cố “Không có hai người nào ngồi cạnh nhau phải đứng dậy”.
- TH1: Không có ai tung được mặt ngửa. Trường hợp này có 1 khả năng xảy ra.
- TH2: Chỉ có 1 người tung được mặt ngửa. Trường hợp này có 8 khả năng xảy ra.
- TH3: Có 2 người tung được mặt ngửa nhưng không ngồi cạnh nhau: Có 8.5 2 = 20 khả năng xảy ra (do mỗi người trong vòng tròn thì có 5 người không ngồi cạnh).
- TH4: Có 3 người tung được mặt ngửa nhưng không có 2 người nào trong 3 người này ngồi cạnh nhau. Trường hợp này có C 8 3 − 8 − 8.4 = 16 khả năng xảy ra.
Thật vậy:
+ Có C 8 3 cách chọn 3 người trong số 8 người.
+ Có 8 khả năng cả ba người này ngồi cạnh nhau.
+ Nếu chỉ có 2 người ngồi cạnh nhau. Có 8 cách chọn ra một người, với mỗi cách chọn ra một người có 4 cách chọn ra hai người ngồi cạnh nhau và không ngồi cạnh người đầu tiên (độc giả vẽ hình để rõ hơn). Vậy có 8.4 khả năng.
- TH5: Có 4 người tung được mặt ngửa nhưng không có 2 người nào trong 4 người này ngồi cạnh nhau. Trường hợp này có 2 khả năng xảy ra.
Suy ra
n A = 1 + 8 + 20 + 16 + 2 = 47 ⇒ P A = 47 256