Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Chọn 10 tấm bất kì có C 30 10
trong 30 thẻ có 15 thẻ mang số chẵn
15 thẻ mang số lẻ và 3 số chia hết cho 10
Ta chọn 10 tấm thẻ lấy ra có 5 tấm thẻ mang số lẻ và 5 tấm thẻ mang số chẵn
trong đó chỉ có 1 tấm mang số chia hết cho 10 có
![]()
Do đó xác suất cần tìm là
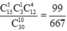

Đáp án A
Chọn 10 tấm bất kỳ có: C 30 10 , trong 30 thẻ có 15 thẻ mang số chẵn, 15 thẻ mang số lẻ và 3 số chia hết cho 10.
Ta chọn 10 tấm thẻ lấy ra 5 tấm thẻ mang số lẻ và 5 tấm thẻ mang số chẵn, trong đó chỉ có một tấm mang số chia hết cho 10 có: C 15 5 . C 3 1 . C 12 4 cách
Do đó xác suất cần tìm là: C 15 5 . C 3 1 . C 12 4 C 30 10 = 99 667 .

Đáp án C
Chọn ra 8 tấm thẻ 1 cách ngẫu nhiên có ![]() cách
cách
Trong 20 tấm thẻ có 10 tấm mang số lẻ, có 5 tấm mang số chẵn không chia hết cho 4 và 5 tấm thẻ mang số chẵn chia hết cho 4
TH1: Lấy được 5 tấm mang số lẻ, 2 tấm mang số chẵn chia hết cho 4 và tấm mang 1 số chẵn không chi hết cho 4 có: ![]()
TH2: Lấy được 5 tấm mang số lẻ, 3 tấm mang số chẵn chia hết cho 4 có ![]() cách.
cách.
Vậy xác suất cần tìm là
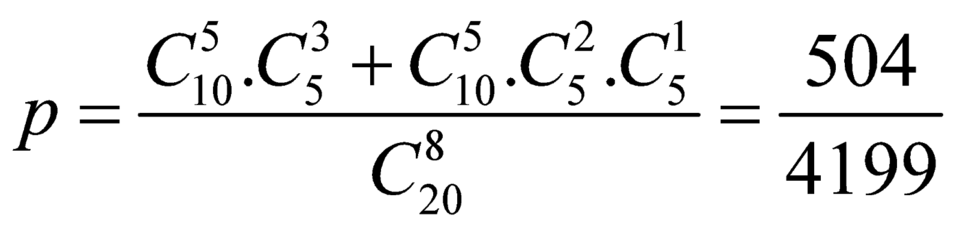

Haizz. Mik cx tham khảo rồi. Cái quan trọng là chọn chia hết cho 3

Không gian mẫu: \(C_{15}^5\)
Tổng số 5 tấm thẻ là lẻ khi số số thẻ lẻ là 1 số lẻ, gồm các trường hợp: (1 thẻ lẻ, 4 thẻ chẵn), (3 thẻ lẻ, 2 thẻ chẵn), (5 thẻ đều lẻ)
Trong 15 tấm thẻ có 7 thẻ chẵn và 8 thẻ lẻ
\(\Rightarrow\) Số biến cố thuận lợi: \(C_8^1.C_7^4+C_8^3.C_7^2+C_8^5\)
Xác suất: ...


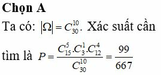

gọi\(\Omega\) là không gian mẫu để rút ra 10 tấm thẻ trong 30 tấm==>n(\(\Omega\))=C1030 =30045015
gọi A là biến cố "lấy 10 tấm thẻ trong đó có 5 tấm mang số lẻ, 5 tấm chẵn trong đó có 1 tấm chia hết cho 10"
nx: có 30 tấm đánh số từ 1->30 ------->15 tấm lẻ, 15 tấm chẵn, có 3 tấm chứa số 10, 20,30 là chia hết cho 10
- trường hợp rút 5 tấm lẻ là :C515 =3003 cách
- TH rút 5 tấm chẵn trong đó có 1 tấm chia hết cho 10 là
3xC412 =1485 cách
=======> n(A)=1485x3003=4459455 cách====>P(A)=99/667