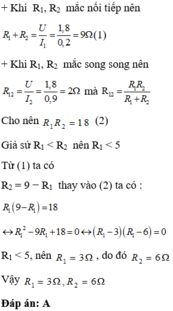Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, Khi 3 điện trở mắc song song thì UAB=U1=U2=U3
=> I1R1=I2R2=I3R3 => 3R1 = R2 = 1,5R3
=> R2 = 3R1 ; R3= 2R1
Khi 3 điệm trở mắc nối tiếp Rm=R1+R2+R3=6R1
=> Cường độ dòng điện chạy qua mỗi điện trở là:
I1=I2=I3= UAB/(6R1) = 3/6=1/2 (A)
Vì R 1 mắc song song R 2 nên: U 1 = U 2 ⇔ I 1 . R 1 = I 1 . R 2
Mà I 1 = 1,5 I 2 → 1,5 I 2 . R 1 = I 2 . R 2 → 1,5 R 1 = R 2
Từ (1) ta có R 1 + R 2 = 10Ω (2)
Thay R 2 = 1,5 R 1 vào (2) ta được: R 1 + 1,5 R 1 = 10 ⇒ 2,5 R 1 = 10 ⇒ R 1 = 4Ω
⇒ R 2 = 1,5.4 = 6Ω
Khi R1 mắc nối tiếp với R2 thì: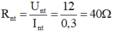 
↔ R1 + R2 = 40Ω (1)
Khi R1 mắc song song với R2 thì:
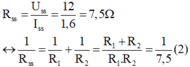
Thay (1) vào (2) ta được R1.R2 = 300
Ta có: R2 = 40 – R1 → R1.(40 – R1) = 300 ↔ - R12 + 40R1 – 300 = 0 (*)
Giải (*) ta được: R1 = 30Ω; R2 = 10Ω hoặc R1 = 10Ω; R2 = 30Ω.
R 1 + R 2 = U / I = 40 ( R 1 . R 2 ) / ( R 1 + R 2 ) = U / I ’ = 7 , 5
Giải hệ pt theo R 1 ; R 2 ta được R 1 = 30 ; R 2 = 10
Hoặc R 1 = 10 ; R 2 = 30
Hai điện trở mắc song song nhau.
Dòng điện qua mạch: \(I=I_1+I_2\)
Dòng điện chạy qua \(R_1\) là: \(I_1=I-I_2=1,2-0,5=0,7A\)
R 1 nối tiếp R 2 nên điện trở tương đương của mạch lúc này là:
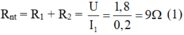
R 1 song song với R 2 nên điện trở tương đương của mạch lúc này là:
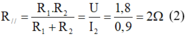
Lấy (1) nhân với (2) theo vế ta được
R
1
.
R
2
= 18 →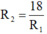 
(3)
Thay (3) vào (1), ta được: R 12 - 9 R 1 + 18 = 0
Giải phương trình, ta có: R 1 = 3Ω; R 2 = 6Ω hay R 1 = 6Ω; R 2 = 3Ω
Khi mắc nối tiếp:
\(R_{tđ}=R_1+R_2=\dfrac{U}{I}=\dfrac{24}{0,6}=40\left(\Omega\right)\left(1\right)\)
Khi mắc song song:
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{12}{1,6}=\dfrac{15}{2}\Rightarrow R_1.R_2=\dfrac{15}{2}.40=300\left(\Omega\right)\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow\left\{{}\begin{matrix}R_1+R_2=40\left(\Omega\right)\\R_1.R_2=300\left(\Omega\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}R_1=\dfrac{300}{R_2}\\\dfrac{300}{R_2}+R_2=40\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}R_1=\dfrac{300}{R_2}\\\dfrac{300+R_2^2}{R_2}=40\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}R_1=\dfrac{300}{R_2}\\\left(R_2-30\right)\left(R_2-10\right)=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}R_1=10\left(\Omega\right)\\R_2=30\left(\Omega\right)\end{matrix}\right.\\\left\{{}\begin{matrix}R_1=30\left(\Omega\right)\\R_2=10\left(\Omega\right)\end{matrix}\right.\end{matrix}\right.\)