Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Các điện tích q 1 v à q 2 gây ra tại C các véc tơ cường độ điện trường E 1 → và E 2 → có phương chiều như hình vẽ:
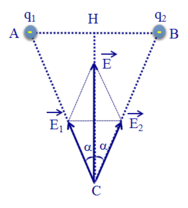
Có độ lớn: E 1 = E 2 = k | q 1 | A C 2 = 9.10 9 .8.10 − 6 0 , 25 2 = 11 , 52 . 10 5 (V/m);
Cường độ điện trường tổng hợp tại C là: E → = E 1 → + E 2 → có phương chiều như hình vẽ, có độ lớn:
E = E 1 . cos α + E 2 cos α = 2 E 1 cos α = 2 E 1 C H A C = 2 . 11 , 52 . 10 5 . 25 2 − 10 2 25 = 21 , 12 . 10 5 ( V / m )
b) Điện tích q 3 đặt tại H gây ra tại C véc tơ cường độ điện trường E ' → sao cho E → + E ' → = 0 → ð E → = - E ' → . Để thoả mãn điều đó thì q 3 < 0 và có độ lớn:
| q 3 | = E . H C 2 k = 11 , 52.10 5 . ( 0 , 25 2 − 0 , 1 2 ) 9.10 9 = 6 , 72 . 10 - 6 .
Vậy q 3 = 6 , 72 . 10 - 6 C.

a) Các điện tích q 1 v à q 2 gây ra tại M các véc tơ cường độ điện trường E 1 → và E 2 → có phương chiều như hình vẽ.
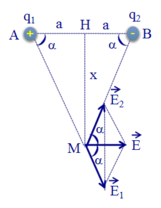
Có độ lớn: E 1 = E 2 = k q ε ( a 2 + x 2 )
Cường độ điện trường tổng hợp tại M do các điện tích q 1 v à q 2 gây ra là:
E → = E 1 → + E 2 → ; có phương chiều như hình vẽ.
Có độ lớn: 2 E 1 cos α = 2 . k q ( a 2 + x 2 ) a a 2 + x 2 = 2 k q a ( a 2 + x 2 ) 3 2
b) Theo câu a ta có: E = 2 k q a ( a 2 + x 2 ) 3 2 ; để E có giá trị cực đại thì mẫu số phải có giá trị cực tiểu mà mẫu số có giá trị cực tiểu khi x = 0 tức là M trùng với H.

Đáp án: A
Vì cường độ điện trường tại M bằng 0 nên hai vecto E 1 do q1 gây ra và E 2 do q2 gây ra phải ngược chiều và cùng độ lớn nên M nằm trên đường thẳng AB
r1 < r2 và r1 + AB = r2 nên q1 và q2 trái dấu và |q1| < |q2|
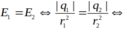
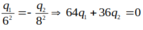
và q1 + q2 = 7.10-8
=> q1= -9.10-8 C, q2= 16.10-8 C

a) Các điện tích q1 và q2 gây ra tại M các véc tơ cường độ điện trường E 1 → và E 2 → có phương chiều như hình vẽ:

Có độ lớn: E 1 = E 2 = k q ( a 2 + x 2 ) .
Cường độ điện trường tổng hợp tại M do các điện tích q 1 v à q 2 gây ra là:
E → = E 1 → + E 2 → ; có phương chiều như hình vẽ.
Có độ lớn: E = E 1 cos α + E 2 cos α = 2 E 1 cos α = 2 . k q ( a 2 + x 2 ) . x a 2 + x 2 = 2 k q x ( a 2 + x 2 ) 3 2
b) Theo câu a ta có E = 2 k q x ( a 2 + x 2 ) 3 2 = 2 k q a 2 x 2 3 + x 4 3 3 2 .
Để E có giá trị cực đại thì mẫu số phải có giá trị cực tiểu mà mẫu số có giá trị cực tiểu khi a 2 x 2 3 = x 4 3 (theo bất đẳng thức Côsi) ð a 2 = x 2 hay x = a.

Chọn: D
Hướng dẫn:
Hai điện tích điểm q 1 = 0,5 (nC) = 5 . 10 - 10 (C) và q 2 = - 0,5 (nC) = - 5 . 10 - 10 (C) đặt tại hai điểm A, B cách nhau 6 (cm) trong không khí. Xét điểm M nằm trên đường trung trực của AB cách trung điểm của AB một khoảng 4 (cm), ta có AM = BM = r = 5 (cm) = 0,05 (m).
- Cường độ điện trường do q 1 = 5 . 10 - 10 (C) đặt tại A, gây ra tại M là
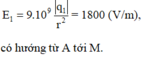
- Cường độ điện trường do q 2 = - 5 . 10 - 10 (C) đặt tại B, gây ra tại M là
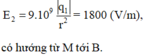
- Cường độ điện trường tổng hợp tại điểm M là


Ta có AM = BM = A H 2 + H M 2 = 12 2 + 16 2 = 20 (cm)
Các điện tích q 1 v à q 2 gây ra tại M các véc tơ cường độ điện trường E 1 → và E 2 → có phương chiều như hình vẽ.
Có độ lớn: E 1 = E 2 = k | q 1 | A M 2 = 9.10 9 .9.10 − 6 0 , 2 2 = 20 , 25 . 10 5 (V/m).
Cường độ điện trường tổng hợp tại M là: E → = E 1 → + E 2 → .
Có phương chiều như hình vẽ.
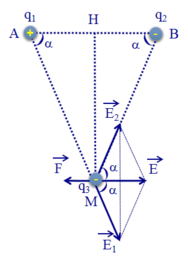
Có độ lớn: E = E 1 cos α + E 2 cos α = 2 E 1 cos α
= 2 E 1 A H A M = 2 . 20 , 25 . 10 5 12 20 = 24 , 3 . 10 5 (V/m).
F → = q 3 E → ; vì q 3 < 0 nên F → cùng phương ngược chiều với E → và có độ lớn:
F = q 3 E = 5 . 10 - 8 . 24 , 3 . 10 5 = 0 , 1215 (N).


với EM = 0 áp dụng nguyên ký chồng chất điện trường: E1 +E2 =0 \(\Rightarrow\) \(\begin{cases}E_1=E_2\\\overrightarrow{E}_1\uparrow\downarrow\overrightarrow{E}_2\circledast\end{cases}\) TỪ\(\circledast\) và :\(\left|q_1\right|\) < \(\left|q_2\right|\) \(\Rightarrow\) M nằm trên AB và bên phía A
\(\Rightarrow\) -r1 +r2 =30 \(\otimes\)
lại có: E1 =E2 \(\Rightarrow\) k* \(\frac{\left|q_1\right|}{r^2_1}\)= k* \(\frac{\left|q_2\right|}{r^2_2}\)
\(\Leftrightarrow\)\(\frac{1}{r^2_1}\)= \(\frac{4}{r^2_2}\)\(\Rightarrow\)2 r1 -r2 = 0 \(\left(\otimes\otimes\right)\)
giải hệ pt \(\otimes\) và \(\left(\otimes\otimes\right)\) , ta được r1 =30; r2 =60
vậy M cách A 30cm
và cách B 60cm