Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Không gian mẫu Ω có số phần tử là n Ω = 10 ! .
Gọi A là biến cố “Xếp được dòng chữ “NƠI NÀO CÓ Ý CHÍ NƠI ĐÓ CÓ CON ĐƯỜNG”. Số phần tử của biến cố A là n A = 1 .
Vậy xác suất cần tính là P A = n A n Ω = 1 10 ! = 1 3628800 .


Gọi A: “mỗi nhóm có đúng một học sinh nữ”.
+) Số cách xếp 3 học sinh nữ vào 3 nhóm là 3! cách.

+) Chọn 3 học sinh nam cho nhóm thứ ba có 1 cách.
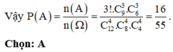

Đáp án A
Không gian mẫu: C 12 4 . C 8 4 . 1 = 34650
Chỉ có 3 nữ và chia mỗi nhóm có đúng 1 nữ và 3 nam.
Nhóm 2 có C 3 1 . C 9 3 = 252 cách.
Lúc đó còn lại 2 nữ, 6 nam, nhóm thứ 2 có :
C 2 1 . C 9 3 = 40 cách chọn.
Cuối cùng còn 4 người là một nhóm: có 1 cách.
Theo quy tắc nhân thì có: 252.40.2=10080 cách.
Vậy xác suất cần tìm là: P = 10080 34650 = 16 55 .

Chọn B.
Kí hiệu học sinh lớp 12A, 12B, 12C lần lượt là A, B, C.
Số phần tử không gian mẫu là n(Ω)=9!
Gọi E là biến cố các học sinh cùng lớp luôn ngồi cạnh nhau. Ta có các bước sắp xếp như sau:
- Xếp 5 học sinh lớp 12C ngồi vào bàn sao cho các học sinh này ngồi sát nhau. Số cách sắp xếp là 5!
- Xếp 3 học sinh lớp 12B vào bàn sao cho các học sinh này ngồi sát nhau và sát nhóm của học sinh 12C. Số cách sắp xếp là 3!.2
- Xếp 2 học sinh lớp 12A vào hai vị trí còn lại của bàn. Số cách sắp xếp là 2!
Số phần tử thuận lợi cho biến cố E là n(E)=5!.3!.2.2!
Xác suất của A là P ( E ) = n ( E ) n ( Ω ) = 1 126

Đáp án B
Số phần tử KGM là: 9!. Mà số phần tử của biến cố các học sinh nữ luôn ngồi cạnh nhau là: 3!7!
Xác suất để các học sinh nữ luôn ngồi cạnh nhau là: 3!7! 9! = 1 12
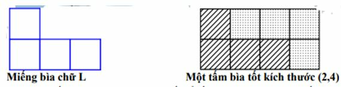




Chọn D