Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

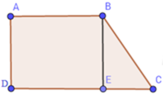
Tứ giác ABED có A ^ = D ^ = E ^ = 90 0 nên là hình chữ nhật. Suy ra DE = AB = 10 cm. Do đó: EC = DC – DE = 13 – 10 = 3 (cm)
Ta có:
SBEC = 1 2 BE. EC => BE = 2 S B E C E C = 2.13 , 5 3 = 9 (cm)
SABED = AB.BE = 10.9 = 90 (cm2)
SABCD = SABED + SBEC = 90 + 13, 5 = 103, 5 (cm2).
Đáp án cần chọn là: A

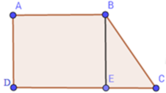
Tứ giác ABED có A ^ = B ^ = E ^ = 900 nên là hình chữ nhật. Suy ra DE = AB = 9 cm.
Do đó: EC = DC – DE = 13, 5 – 9 = 4, 5 (cm)
Ta có:
SBEC = 1 2 BE. EC => BE = 2 S B E C E C = 2.18 4 , 5 = 8 (cm)
SABED = AB.BE = 9.8 = 72 (cm2)
SABCD = SABED + SBEC = 72 + 18 = 90 (cm2).
Đáp án cần chọn là: C

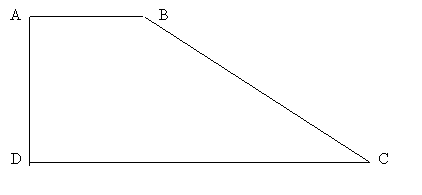
* Xét diện tích tam giác ABD và diện tích tam giác BCD ta có :
- Chiều cao hạ từ đỉnh D của tam giác ADB bằng chiều cao hạ từ đỉnh B của tam giác BCD.
- Đáy AB = 1/3 CD
Nên diện tích tam giác ABD bằng 1/3 diện tích tam giác BCD
=> S_ABD = 1/4 S_ABCD = 1/4 x 72 = 18 cm2
* Xét diện tích tam giác ABD và diện tích tam giác BCD ta có :
- Chiều cao hạ từ đỉnh D của tam giác ADB bằng chiều cao hạ từ đỉnh B của tam giác BCD.
- Đáy AB = 1/3 CD
Nên diện tích tam giác ABD bằng 1/3 diện tích tam giác BCD
=> S_ABD = 1/4 S_ABCD = 1/4 x 72 = 18 cm2

Kéo dài AB về phía B một đoạn BE=DC. Nối DE cắt BC tại M.
Do CD // BE nên ta có tam giác MDC = tam giác MEB (trường hợp g.c.g). Suy ra dt(ABCD)=dt(ABMD) + dt(MDC) = dt(ABMD) + dt(MEB) = dt(DAE) = 1/2 .AE . h =1/2 (AB + BE).h = \(\dfrac{AB+CD}{2}.h\)
b) Theo câu a) thì diện tích hình thang ABCD bằng diện tích tam giác DAE nên ta nối D với trung điểm N của AE thì DN sẽ chia tam giác DAE thành 2 phần bằng nhau. Khi đó diện tích tam giác DAN bằng nửa diện tích hình thang ABCD.

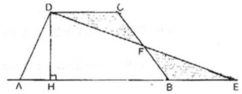
Gọi F là trung điểm của cạnh bên BC. Cắt hình thang theo đường DF đưa ghép về như hình vẽ bên, điểm C trung với điểm B, D trùng với E.
Vì AB // CD ⇒ ∠ (ABC) = 180 0 ⇒ A, B, E thẳng hàng
∠ (ABF) + ∠ (DFC) = 180 0
⇒ D, F, E thẳng hàng
△ DFC = △ EFB (g.c.g)
S D F C = S E F B
Suy ra: S A B C D = S A D E
△ DFC = △ EFB⇒ DC = BE
AE = AB + BE = AB + DC
S A D E = 1/2 DH. AE = 1/2 DH. (AB + CD)
Vậy : S A B C D = 1/2 DH. (AB + CD)