
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


6x+11y chia hết cho 31
=> 6x + 11y + 31y chia hết cho 31 (vì 31y cũng chia hết cho 31)
=> 6x + 42y chia hết cho 31
=> 6(x+7y) chia hết cho 31
Vì 6 và 31 nguyên tố cũng nhau nên x+7y cũng phải chia hết cho 31 (ĐPCM)



Có: 6x+11y⋮31⇒6(6x+11y)⋮316x+11y⋮31⇒6(6x+11y)⋮31
⇒36x+66y⋮31⇒31x+31y+5x+35y⋮31⇒36x+66y⋮31⇒31x+31y+5x+35y⋮31
⇒31(x+y)+5(x+7y)⇒31(x+y)+5(x+7y)
⇒31(x+y)⋮31⇒5(x+7y)⋮31⇒31(x+y)⋮31⇒5(x+7y)⋮31
Mà ƯCLN (5,31) = 1
Vậy: x + 7y chia hết cho 31
Vậy x + 7y là bội 31
CHÚC HỌC GIỎI

6x+11y chia hết cho 31
=> 6x + 11y + 31y chia hết cho 31 (vì 31y cũng chia hết cho 31)
=> 6x + 42y chia hết cho 31
=> 6(x+7y) chia hết cho 31
Vì 6 và 31 nguyên tố cũng nhau nên x+7y buộc phải chia hết cho 31 (ĐPCM)
6x+11y chia hết cho 31
=> 6x + 11y + 31y chia hết cho 31 (vì 31y cũng chia hết cho 31)
=> 6x + 42y chia hết cho 31
=> 6(x+7y) chia hết cho 31
Vì 6 và 31 nguyên tố cũng nhau nên x+7y buộc phải chia hết cho 31 (ĐPCM)
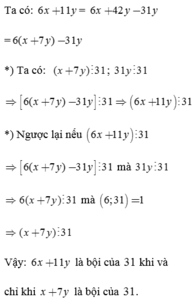
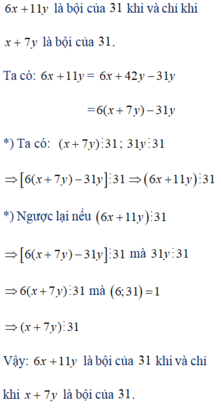
A)\(\left(3x+7y\right)⋮31\Rightarrow\left(15x+35y\right)⋮31\Rightarrow\left[31\left(x+y\right)+31y-\left(16x+27y\right)\right]⋮31\)
\(x;y\in N\Rightarrow\left\{{}\begin{matrix}31\left(x+y\right)⋮31\\31y⋮31\\\end{matrix}\right.\) \(\Rightarrow\left(16x+27y\right)⋮31\)
B)
\(\left(16x+27y\right)⋮31\Rightarrow\left[31x+62y-\left(15x+35y\right)\right]⋮31\Rightarrow\left[31x+62y-5\left(3x+7y\right)\right]⋮31\)\(x;y\in N\Rightarrow\left\{{}\begin{matrix}31x⋮31\\62y⋮31\\5⋮̸31\end{matrix}\right.;\left(5;31\right)=1}\)\(x;y\in N\Rightarrow\left\{{}\begin{matrix}31\left(x+y\right)⋮31\\31y⋮31\\5⋮̸31\end{matrix}\right.\) ; \(\left(5;31\right)=1\Rightarrow\left(3x+7y\right)⋮31\)
từ (A) và (B) : \(\left(3x+7y\right)⋮31\Leftrightarrow\left(16x+27y\right)⋮31\) =>dpcm \(\Leftrightarrow dccm\)