HP
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 11 2023
a:
Sửa đề: \(I\left(\dfrac{1}{2};-3\right)\)
Thay \(x=\dfrac{1}{2};y=-3\) vào (d): \(y=\left(1-2m\right)x+m-\dfrac{7}{2}\), ta được:
\(\left(1-2m\right)\cdot\dfrac{1}{2}+m-\dfrac{7}{2}=-3\)
=>\(\dfrac{1}{2}-m+m-\dfrac{7}{2}=-3\)
=>\(\dfrac{1}{2}-\dfrac{7}{2}=-3\)
=>-3=-3(đúng)
vậy: I(1/2;-3) là điểm cố định mà (d): \(y=\left(1-2m\right)x+m-\dfrac{7}{2}\) luôn đi qua
b: \(\left(d\right):y=\left(2m+1\right)x+m-2\)
\(=2mx+x+m-2\)
\(=m\left(2x+1\right)+x-2\)
Điểm mà (d) luôn đi qua có tọa độ là:
\(\left\{{}\begin{matrix}2x+1=0\\y=x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=-\dfrac{1}{2}-2=-\dfrac{5}{2}\end{matrix}\right.\)
CM
30 tháng 9 2018
c) Giả sử đường thẳng d 1 luôn đi qua một điểm cố định ( x 1 ; y 1 ) với mọi giá trị của m.
⇒ y 1 = m x 1 + 2m - 1 với mọi m
⇔ m( x 1 + 2) - 1 - y 1 = 0 với mọi m
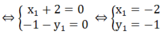
Vậy điểm cố định mà d 1 luôn đi qua với mọi giá trị của m là (-2; -1).
TQ
1
29 tháng 10 2021
Gọi \(A\left(x_0;y_0\right)\) là điểm cố định mà \(\left(d\right)\) luôn đi qua
\(\Leftrightarrow y_0=\left(1+m\right)x_0-2m+4=x_0+mx_0-2m+4\\ \Leftrightarrow m\left(x_0-2\right)+\left(x_0-y_0+4\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0=2\\2-y_0+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=2\\y_0=6\end{matrix}\right.\)
Vậy \(\left(d\right)\) luôn đi qua \(A\left(2;6\right)\) cố định với mọi m
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 12 2020
Giả sử điểm cố định mà (d) luôn đi qua có tọa độ \(M\left(x_0;y_0\right)\)
\(\Rightarrow\) Với mọi m, ta luôn có:
\(y_0=\left(2m+1\right)x_0+m-2\)
\(\Leftrightarrow m\left(2x_0+1\right)+x_0-y_0-2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x_0+1=0\\x_0-y_0-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_0=-\dfrac{1}{2}\\y_0=-\dfrac{5}{2}\end{matrix}\right.\)
Vậy với mọi m thì (d) luôn đi qua điểm cố định có tọa độ \(\left(-\dfrac{1}{2};-\dfrac{5}{2}\right)\)