
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sai đề rồi nha bạn!
Đề: Cho \(a,b,c>0\) thỏa mãn \(a^2+b^2+c^2=\frac{5}{3}.\) Chứng minh rằng: \(\frac{1}{a}+\frac{1}{b}-\frac{1}{c}<\frac{1}{abc}\)
Lời giải:
Với mọi \(a,b,c\in R\) thì ta luôn có:
\(a^2+b^2+c^2\ge2bc+2ca-2ab\) \(\left(\text{*}\right)\)
Ta cần chứng minh \(\left(\text{*}\right)\) là bất đẳng thức đúng!
Thật vậy, từ \(\left(\text{*}\right)\) \(\Leftrightarrow\) \(a^2+b^2+c^2+2ab-2bc-2ca\ge0\)
\(\Leftrightarrow\) \(\left(a+b-c\right)^2\ge0\) \(\left(\text{**}\right)\)
Bất đẳng thức \(\left(\text{**}\right)\) hiển nhiên đúng với mọi \(a,b,c\) , mà các phép biến đổi trên tương đương
Do đó, bất đẳng thức \(\left(\text{*}\right)\) được chứng minh.
Xảy ra đẳng thức trên khi và chỉ khi \(a+b=c\)
Mặt khác, \(a^2+b^2+c^2=\frac{5}{3}\) (theo giả thiết)
Mà \(\frac{5}{3}=1\frac{2}{3}<2\)
\(\Rightarrow\) \(a^2+b^2+c^2<2\) \(\left(\text{***}\right)\)
Từ \(\left(\text{*}\right)\) kết hợp với \(\left(\text{***}\right)\), ta có thể viết 'kép' lại: \(2bc+2ca-2ab\le a^2+b^2+c^2<2\)
Suy ra \(2bc+2ca-2ab<2\)
Khi đó, vì \(abc>0\) (do \(a,b,c\) không âm) nên chia cả hai vế của bất đẳng trên cho \(2abc\), ta được:
\(\frac{2bc+2ca-2ab}{2abc}<\frac{2}{2abc}\)
\(\Leftrightarrow\) \(\frac{1}{a}+\frac{1}{b}-\frac{1}{c}<\frac{1}{abc}\)
Vậy, với \(a,b,c\) là các số thực dương thỏa mãn điều kiện \(a^2+b^2+c^2=\frac{5}{3}\) thì ta luôn chứng minh được:
\(\frac{1}{a}+\frac{1}{b}-\frac{1}{c}<\frac{1}{abc}\)

Áp dụng bất đẳng thức AM-GM 3 số không âm :
\(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\ge3\sqrt[3]{\frac{abc}{abc}}=3\sqrt[3]{1}=3\)
Dấu "=" xảy ra \(\Leftrightarrow\frac{a}{b}=\frac{b}{c}=\frac{c}{a}\Leftrightarrow a=b=c\)

BÀi 1
D = 4x - 10 - x2= - (x2 - 4x +10) = - (x - 2 )2 - 6
Vì - (x - 2 )2 \(\le0\)nên - (x - 2 )2 - 6 \(\le-6< 0\)
Vậy D = 4x - 10 - x2 luôn âm (dpcm)
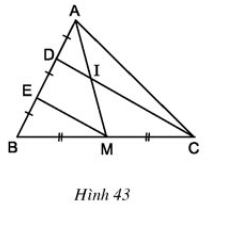 cm: ID=
cm: ID=
Xét tam giác BDC có:
M là trung điểm BC(gt)
E là trung điểm BD(gt)
=> EM là đường trung bình tam giác BDC
=> EM//DC và \(EM=\dfrac{1}{2}DC\left(1\right)\)
Mà \(I\in DC\)
=> EM//DI
Xét tam giác AEM có
EM//DI(cmt)
D là trung điểm AE(gt)
=> I là trung điểm AM
=> DI là đường trung bình tam giác AEM
=> \(DI=\dfrac{1}{2}EM\left(2\right)\)
Từ (1),(2)
=> \(DI=\dfrac{1}{2}.\dfrac{1}{2}DC=\dfrac{1}{4}DC\left(đpcm\right)\)
cam on