Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

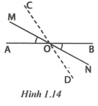
Theo đề bài ta có A O M ^ = M O C ^ , B O N ^ = D O N ^ mà A O M ^ = B O N ^ (hai góc đối đỉnh) nên M O C ^ = D O N ^ .
Ta có M O D ^ + D O N ^ = 180 ° (hai góc kề bù), suy ra M O D ^ + M O C ^ = 180 ° .
Hai góc MOD và MOC là hai góc kề, có tổng bằng 180 ° nên hai tia OC, OD đối nhau.
Chứng tỏ một tia là tia phân giác

O A M D C N B
Ta có:
AB và CD cắt nhau tại O.
=> OA đối OB; OC đối OD.
=> \(\widehat{AOD}\) và \(\widehat{COB}\) là hai góc đối đỉnh.
=> \(\widehat{AOD}=\widehat{COB}\)
Mà: OM là phân giác \(\widehat{AOD}\)
ON là phân giác \(\widehat{COB}\)
=> +) \(\widehat{CON}=\widehat{NOB}=\frac{1}{2}\widehat{COB}\) (1)
+) \(\widehat{AOM}=\widehat{MOD}=\frac{1}{2}\widehat{AOD}\) (2)
Từ (1) và (2) => \(\widehat{CON}=\widehat{NOB}=\widehat{AOM}=\widehat{MOD}\)
Mà AB cắt CD tại O
=> CD cắt MN tại O
=> CON đối đỉnh MOD
=> OC đối OD
OM đối ON
Vậy OM đối ON(đpcm)
đáp án:
Ta có:
AB và CD cắt nhau tại O.
=> OA đối OB; OC đối OD.
=> ˆAODAOD^ và ˆCOBCOB^ là hai góc đối đỉnh.
=> ˆAOD=ˆCOBAOD^=COB^
Mà: OM là phân giác ˆAODAOD^
ON là phân giác ˆCOBCOB^
=> +) ˆCON=ˆNOB=12ˆCOBCON^=NOB^=12COB^ (1)
+) ˆAOM=ˆMOD=12ˆAODAOM^=MOD^=12AOD^ (2)
Từ (1) và (2) => ˆCON=ˆNOB=ˆAOM=ˆMODCON^=NOB^=AOM^=MOD^
Mà AB cắt CD tại O
=> CD cắt MN tại O
=> CON đối đỉnh MOD
=> OC đối OD
OM đối ON
Vậy OM đối ON(đpcm)

ta có : 2 đường thẳng AB và CD cách nhau tại O sẽ tạo ra các góc đối đỉnh
=>AOC=BOD [2 góc đối dỉnh]
TA CÓ: OM và ON lần lượt là tia phân giác của AOC ,BOD
Suy ra OM và ON là 2 tia đối nhau
Ta có: \(\widehat{xOm}=\dfrac{\widehat{xOb}}{2}\)
\(\widehat{yOn}=\dfrac{\widehat{yOa}}{2}\)
mà \(\widehat{xOb}=\widehat{yOa}\)(hai góc đối đỉnh)
nên \(\widehat{xOm}=\widehat{yOn}\)
mà \(\widehat{xOm}+\widehat{mOy}=180^0\)(hai góc kề bù)
nên \(\widehat{yOm}+\widehat{yOn}=180^0\)
=>Om và On là hai tia đối nhau