
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A=1+4+4^2+...+4^59A=1+4+4^2+...+4^59
A=(1+4)+(4^2+4^3)+...+(4^58+4^59)A=(1+4)+(4^2+4^3)+...+(4^58+4^59)
A=(1+4)+4^2(1+4)+...+4^58(1+4)A=(1+4)+4^2(1+4)+...+4^58(1+4)
A=5+4^2.5+...+4^58.5A=5+4^2.5+...+4^58.5
A=5(1+4^2+...+4^48)A=5(1+4^2+...+4^58)
A=5(1+4^2+...+4^58) chia hết cho 5
vậy A chia hết cho 5
A=1+4+4^2+...+4^59A=1+4+4^2+...+4^59
A=(1+4+4^2)+(4^3+4^4+4^5)+...+(4^57+4^58+4^59)A=(1+4+4^2)+(4^3+4^4+4^5)+...+(4^57+4^58+4^59)
A=(1+4+4^2)+4^3(1+4+4^2)+...+4^57(1+4+4^2)A=(1+4+4^2)+4^3(1+4+4^2)+...+4^57(1+4+4^2)
A=21+4^3.21+...+4^57.21A=21+4^3.21+...+4^57.21
A=21(1+4^3+...+4^57)A=21(1+4^3+...+4^57)
A=21(1+4^3+...+4^57) chia hết cho 21
vậy A chia hết cho 21
mik làm xong rồi nhớ k cho mik nha mik cảm ơn

Bài 1:
a) Ta có: \(\left(2x-1\right)^{20}=\left(2x-1\right)^{18}\)
\(\Leftrightarrow\left(2x-1\right)^{20}-\left(2x-1\right)^{18}=0\)
\(\Leftrightarrow\left(2x-1\right)^{18}\left[\left(2x-1\right)^2-1\right]=0\)
\(\Leftrightarrow\left(2x-1\right)^{18}\cdot\left(2x-2\right)\cdot2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\\x=1\end{matrix}\right.\)
b) Ta có: \(\left(2x-3\right)^2=9\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3\\2x-3=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=0\end{matrix}\right.\)
c) Ta có: \(\left(x-5\right)^2=\left(1-3x\right)^2\)
\(\Leftrightarrow\left(x-5\right)^2-\left(3x-1\right)^2=0\)
\(\Leftrightarrow\left(x-5-3x+1\right)\left(x-5+3x-1\right)=0\)
\(\Leftrightarrow\left(-2x-4\right)\left(4x-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{3}{2}\end{matrix}\right.\)
Bài 2:
a) \(15^{20}-15^{19}=15^{19}\left(15-1\right)=15^{19}\cdot14⋮14\)
b) \(3^{20}+3^{21}+3^{22}=3^{20}\left(1+3+3^2\right)=3^{20}\cdot13⋮13\)
c) \(3+3^2+3^3+...+3^{2007}\)
\(=3\left(1+3+3^2\right)+...+3^{2005}\left(1+3+3^2\right)\)
\(=13\left(3+...+3^{2005}\right)⋮13\)

A = 4 + 4² + 4³ + ... + 4²³ + 4²⁴
Số số hạng của A:
24 - 1 + 1 = 24
Do 24 ⋮ 2 nên ta có thể nhóm các số hạng của A thành từng nhóm mà mỗi nhóm có 2 số hạng như sau:
A = (4 + 4²) + (4³ + 4⁴) + ... + (4²³ + 4²⁴)
= 20 + 4².(4 + 4²) + ... + 4²².(4 + 4²)
= 20 + 4².20 + ... + 4²².20
= 20.(1 + 4² + ... + 4²²) ⋮ 20
Vậy A⋮ 20 (1)
Do 24 ⋮ 3 nên ta có thể nhóm các số hạng của A thành từng nhóm mà mỗi nhóm có 3 số hạng như sau:
A = (4 + 4² + 4³) + (4⁴ + 4⁵ + 4⁶) + ... + (4²² + 4²³ + 4²⁴)
= 4.(1 + 4 + 4²) + 4⁴.(1 + 4 + 4²) + ... + 4²².(1 + 4 + 4²)
= 4.21 + 4⁴.21 + ... + 4²².21
= 21.(4 + 4⁴ + ... + 4²²) ⋮ 21
Vậy A ⋮ 21 (2)
Từ (1) và (2) ⇒ A ⋮ 20 . 21 (do 20 và 21 nguyên tố cùng nhau)
⇒ A ⋮ 420
Vậy A chia hết cho 20; 21; 420

\(A=3+3^2+...+3^{60}\)
\(A=\left(3+3^2\right)+...\left(3^{59}+3^{60}\right)\)
\(A=\left(3+3^2\right)+...+3^{58}.\left(3+3^2\right)\)
\(A=12+...+3^{58}.12\)
\(A=12.\left(1+...+3^{58}\right)⋮4\left(đpcm\right)\)
trời ơi có thể giải thích cho tui tại sao 2(1+2+2^2) hông nghĩ mãi mà đếch ra


*Ta có: A\(=2^1+2^2+2^3+2^4+...+2^{2010}\)
\(=\left(2+2^2\right)+2^2\times\left(2+2^2\right)+...+2^{2008}\times\left(2+2^2\right)\)
\(=\left(2+2^2\right)\times\left(1+2^2+2^3+...+2^{2008}\right)\)
\(=6\times\left(2^2+2^3+...+2^{2008}\right)\)
\(=3\times2\times\left(2^2+2^3+...+2^{2008}\right)\)
\(\Rightarrow A⋮3\)
*Ta có: A \(=2^1+2^2+2^3+2^4+...+2^{2010}\)
\(=2\times\left(1+2+2^2\right)+2^4\times\left(1+2+2^2\right)+...+2^{2008}\times\left(1+2+2^2\right)\)
\(=\left(1+2+2^2\right)\times\left(2+2^4+2^7+...+2^{2008}\right)\)
\(=7\times\left(2+2^4+2^7+...+2^{2008}\right)\)
\(\Rightarrow A⋮7\)
Mình sửa lại đề C 1 chút xíu
*Ta có: C \(=3^1+3^2+3^3+3^4+...+3^{2010}\)
\(=\left(3+3^2\right)+3^2\times\left(3+3^2\right)+...+3^{2008}\times\left(3+3^2\right)\)
\(=\left(3+3^2\right)\times\left(1+3^2+3^3+...+3^{2008}\right)\)
\(=12\times\left(1+3^2+3^3+...+3^{2008}\right)\)
\(=4\times3\times\left(1+3^2+3^3+...+3^{2008}\right)\)
\(\Rightarrow C⋮4\)
Các câu khác làm tương tự nhé. Chúc bạn học tốt!

a) \(A=2^1+2^2+2^3+2^4+...+2^{2010}\)
\(A=\left(2^1+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{2009}+2^{2010}\right)\)
\(A=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{2009}\left(1+2\right)\)
\(A=3\left(2+2^3+...+2^{2009}\right)⋮3\)
\(A=2^1+2^2+2^3+2^4+...+2^{2010}\)
\(A=\left(2^1+2^2+2^3\right)+\left(2^4+2^5+2^6\right)+...+\left(2^{2008}+2^{2009}+2^{2010}\right)\)
\(A=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{2008}\left(1+2+2^2\right)\)
\(A=7\left(2^1+2^4+...+2^{2008}\right)⋮7\)
Các ý dưới bạn làm tương tự nhé.
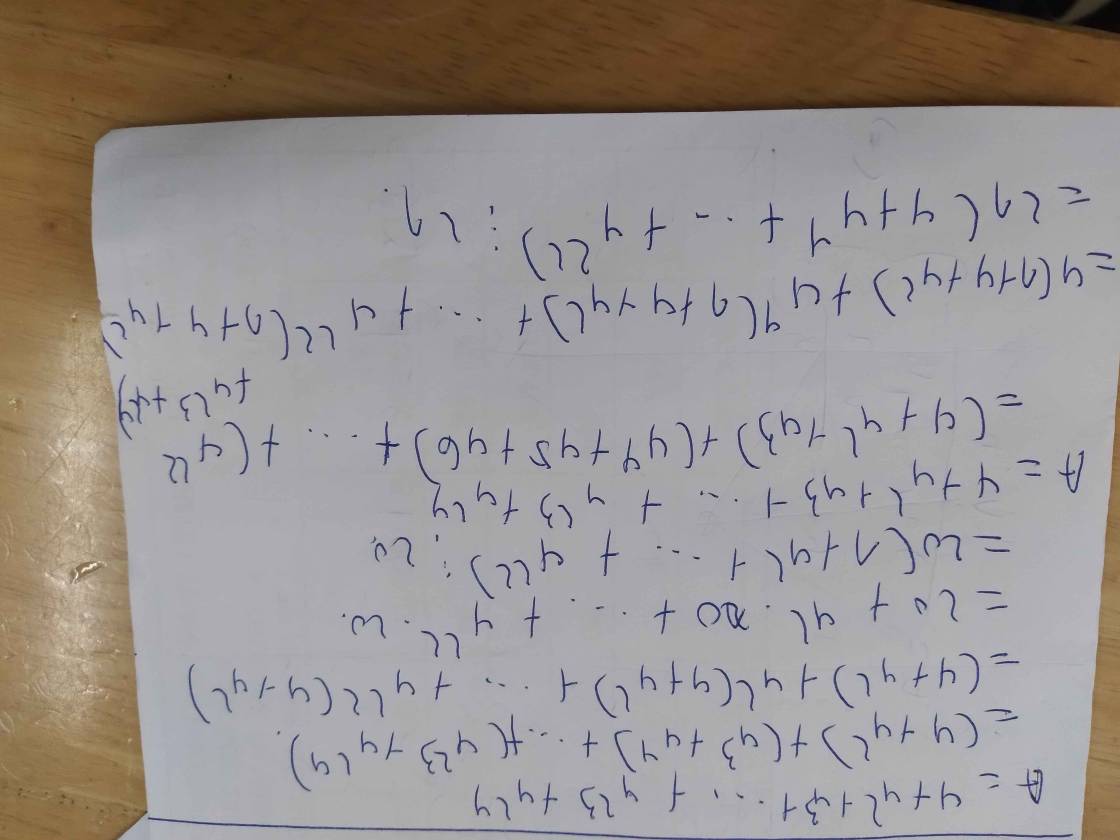
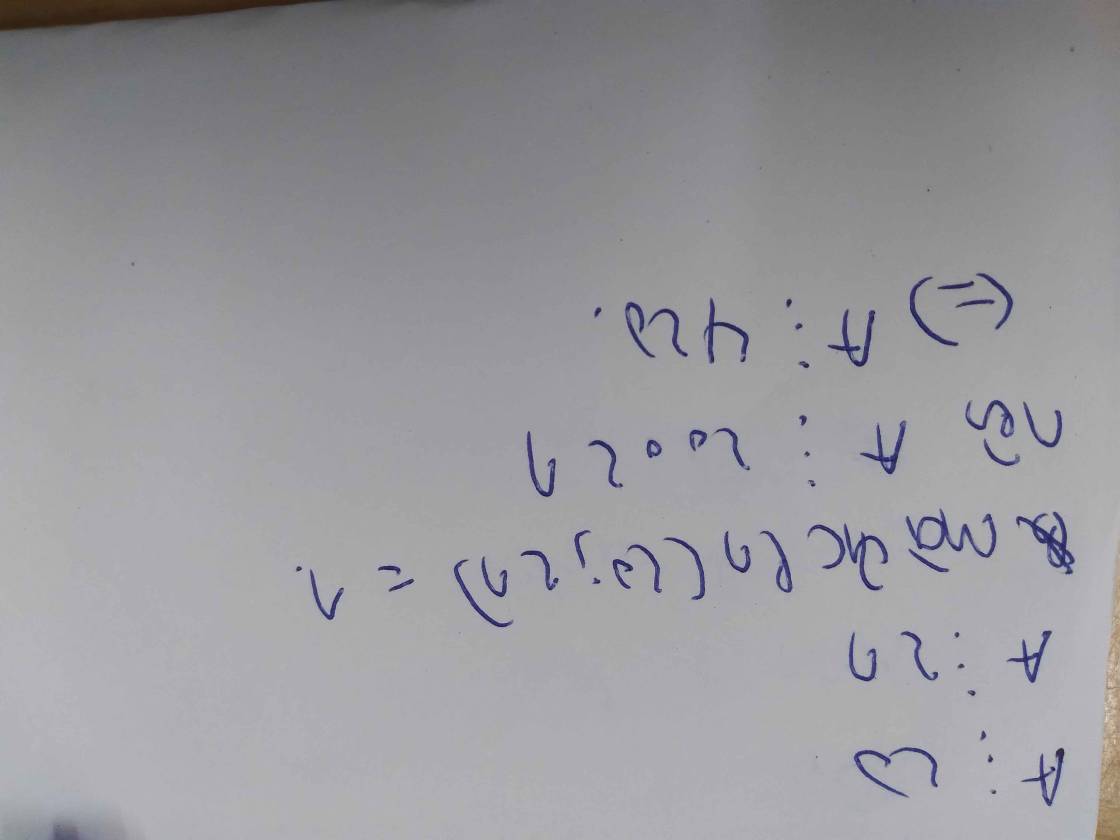
\(A=1+4+4^2+...+4^{2000}\)
\(A=\left(1+4+4^2\right)+4^3\left(1+4+4^2\right)+....+4^{1998}\left(1+4+4^2\right)\)
\(A=21+4^3.21+...+4^{1998}.21\)
\(A=21\left(1+4^3+...+4^{1998}\right)\)
\(\Rightarrow A⋮21\)